四.十字链表法存储有向图

十字链表动态演示 Orthogonal List Demo
→
逻辑结构图 (可拖拽/滚动)
A
B
C
D
十字链表存储结构 (Memory View)
^^^^^^^^A
In
Out
B
In
Out
C
In
Out
D
In
Out
T:A
H:B
hLink
tLink
T:A
H:C
hLink
tLink
T:C
H:D
hLink
tLink
T:D
H:A
hLink
tLink
Struct Definition (C++)
// 弧结点 (ArcBox)
struct ArcBox {
  int tailvex, headvex; // 尾/头顶点位置
  struct ArcBox *hlink; // hLink: 相同弧头(入边)
  struct ArcBox *tlink; // tLink: 相同弧尾(出边)
};

// 顶点结点 (VexNode)
struct VexNode {
  VertexType data;
  ArcBox *firstin;      // firstIn: 第一条入边
  ArcBox *firstout;     // firstOut: 第一条出边
};
操作日志 (Operation Log)
初始化图结构完成...

十字链表法（Orthogonal List）：有向图的高效存储方案 十字链表法是有向图的一种优化存储结构，结合了邻接表和逆邻接表的优势，既能快速访问顶点的出边（邻接表特性），也能快速访问入边（逆邻接表特性），是工程中存储有向图的核心方案之一。本文从核心原理、结构设计、代码实现到特性分析，全面讲解十字链表法。

1、核心概念

1. 定义

十字链表法通过「顶点表 + 边表」的组合结构存储有向图：

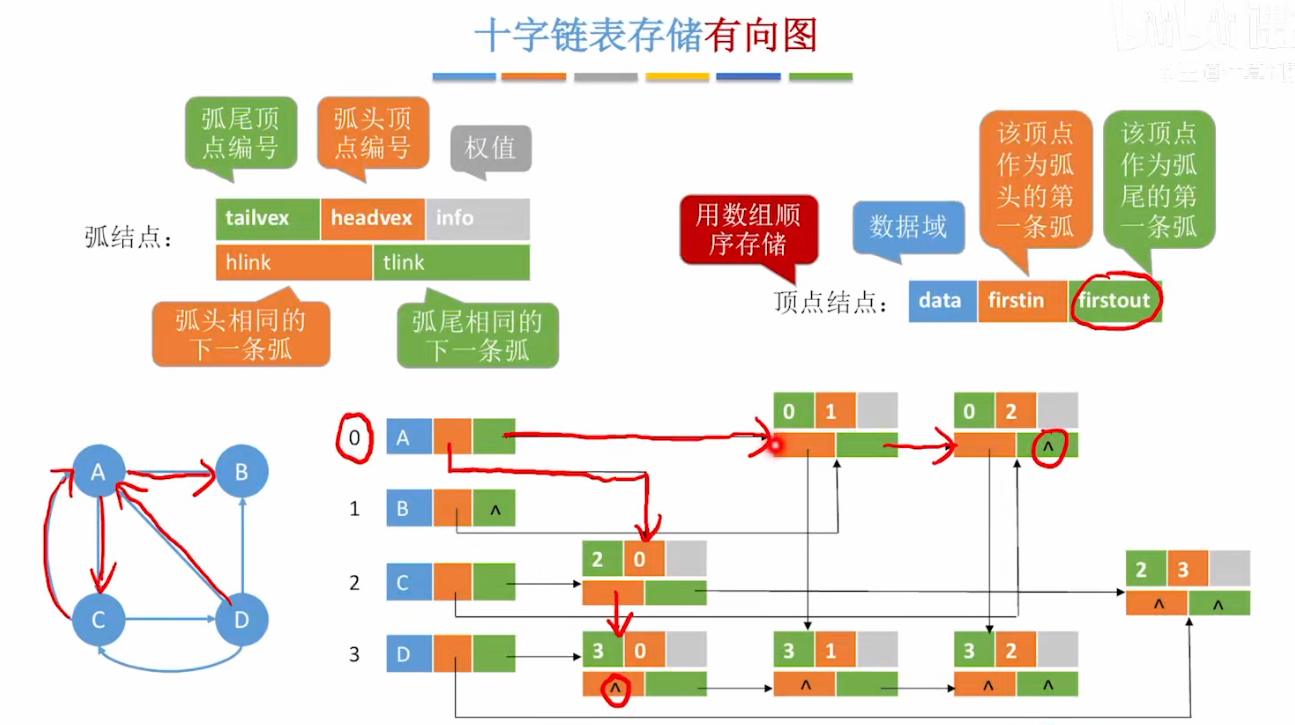
顶点表：一维数组存储所有顶点，每个顶点节点包含「顶点值」「第一个出边指针」「第一个入边指针」；
边表：链表结构存储所有有向边，每个边节点包含「起点索引（tailvex）」「终点索引（headvex）」「同起点下一条出边指针（hlink）」「同终点下一条入边指针（tlink）」，若为带权图可新增「权重（weight）」字段。

2. 核心解决的问题

有向图的传统存储方案存在明显短板：

邻接表：快速查出边，但查入边需遍历所有顶点的邻接链表（时间复杂度O(n+e)）；
逆邻接表：快速查入边，但查出边效率低；
十字链表：同时整合出边/入边的访问能力，空间复杂度与邻接表相当，且兼顾两类查询效率。

3. 核心术语

术语	说明
顶点表节点	存储顶点值 + 指向该顶点「第一条出边」的指针 + 指向该顶点「第一条入边」的指针
边表节点	存储起点索引（tailvex）、终点索引（headvex）、同起点下一出边（hlink）、同终点下一入边（tlink）
出边链表	同一顶点作为起点的所有边，通过hlink指针串联（对应邻接表的出边链）
入边链表	同一顶点作为终点的所有边，通过tlink指针串联（对应逆邻接表的入边链）

2、结构设计（核心）

1. 顶点表节点结构

// 十字链表的顶点表节点
typedef struct VexNode {
    int data;                // 顶点值（可替换为char/自定义类型）
    struct ArcNode *firstin; // 指向该顶点的第一条入边
    struct ArcNode *firstout;// 指向该顶点的第一条出边
} VexNode;

2. 边表节点结构

// 十字链表的边表节点（有向边）
typedef struct ArcNode {
    int tailvex;             // 边的起点（尾顶点）在顶点表中的索引
    int headvex;             // 边的终点（头顶点）在顶点表中的索引
    struct ArcNode *hlink;   // 指向同起点的下一条出边（出边链表的后继）
    struct ArcNode *tlink;   // 指向同终点的下一条入边（入边链表的后继）
    // int weight;            // 带权图新增：边的权重
} ArcNode;

3. 十字链表整体结构

// 十字链表（有向图）
typedef struct {
    VexNode xList[MAX_VERTEX_NUM]; // 顶点表（十字链表的核心数组）
    int vexnum, arcnum;            // 顶点数、边数
} OLGraph;

4. 结构示意图（有向图示例）

以有向图 0→1，0→2，1→2 为例，十字链表的结构如下：

顶点表（数组）：
索引0 → 顶点值0 → firstout→边(0→1) → hlink→边(0→2) → NULL
        → firstin→NULL（无入边）
索引1 → 顶点值1 → firstout→边(1→2) → NULL
        → firstin→边(0→1) → NULL
索引2 → 顶点值2 → firstout→NULL（无出边）
        → firstin→边(0→2) → tlink→边(1→2) → NULL

边表节点：
边(0→1)：tailvex=0，headvex=1 → hlink=边(0→2)，tlink=NULL
边(0→2)：tailvex=0，headvex=2 → hlink=NULL，tlink=边(1→2)
边(1→2)：tailvex=1，headvex=2 → hlink=NULL，tlink=NULL

3、完整代码实现（C语言）

1. 基础定义与辅助函数

#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX_NUM 100  // 最大顶点数

// 边表节点（前置声明，解决指针引用问题）
struct ArcNode;

// 顶点表节点
typedef struct VexNode {
    int data;
    struct ArcNode *firstin;
    struct ArcNode *firstout;
} VexNode;

// 边表节点
typedef struct ArcNode {
    int tailvex;   // 起点索引
    int headvex;   // 终点索引
    struct ArcNode *hlink;
    struct ArcNode *tlink;
    // int weight;  // 带权图可启用
} ArcNode;

// 十字链表结构
typedef struct {
    VexNode xList[MAX_VERTEX_NUM];
    int vexnum, arcnum;
} OLGraph;

// 辅助函数：根据顶点值查找其在顶点表中的索引
int LocateVex(OLGraph *G, int v) {
    for (int i = 0; i < G->vexnum; i++) {
        if (G->xList[i].data == v) {
            return i;
        }
    }
    return -1;  // 顶点不存在
}

2. 核心操作：初始化十字链表

// 初始化十字链表（有向图）
void InitOLGraph(OLGraph *G) {
    printf("请输入有向图的顶点数和边数：");
    scanf("%d%d", &G->vexnum, &G->arcnum);

    // 步骤1：初始化顶点表
    for (int i = 0; i < G->vexnum; i++) {
        printf("请输入顶点%d的值：", i);
        scanf("%d", &G->xList[i].data);
        G->xList[i].firstin = NULL;   // 初始无入边
        G->xList[i].firstout = NULL;  // 初始无出边
    }

    // 步骤2：初始化边表（逐条添加有向边）
    for (int k = 0; k < G->arcnum; k++) {
        int v1, v2;
        printf("请输入有向边<v1, v2>的起点和终点值：");
        scanf("%d%d", &v1, &v2);

        // 查找顶点对应的索引（tail=起点索引，head=终点索引）
        int tail = LocateVex(G, v1);
        int head = LocateVex(G, v2);
        if (tail == -1 || head == -1) {
            printf("顶点不存在，重新输入该边！\n");
            k--;  // 回退，重新输入
            continue;
        }

        // 步骤2.1：创建新的边表节点
        ArcNode *p = (ArcNode *)malloc(sizeof(ArcNode));
        p->tailvex = tail;
        p->headvex = head;
        p->hlink = NULL;
        p->tlink = NULL;
        // p->weight = w; // 带权图需输入权重并赋值

        // 步骤2.2：将新边插入「起点tail的出边链表」（头插法）
        // 逻辑：新边的hlink指向tail原firstout，再更新tail的firstout为新边
        p->hlink = G->xList[tail].firstout;
        G->xList[tail].firstout = p;

        // 步骤2.3：将新边插入「终点head的入边链表」（头插法）
        // 逻辑：新边的tlink指向head原firstin，再更新head的firstin为新边
        p->tlink = G->xList[head].firstin;
        G->xList[head].firstin = p;
    }
}

3. 遍历操作：输出顶点的出边/入边

// 遍历十字链表：输出每个顶点的出边和入边
void PrintOLGraph(OLGraph *G) {
    printf("\n===== 十字链表遍历结果 =====\n");
    for (int i = 0; i < G->vexnum; i++) {
        printf("顶点%d（值：%d）：\n", i, G->xList[i].data);

        // 输出出边（firstout + hlink）
        printf("  出边：");
        ArcNode *p_out = G->xList[i].firstout;
        if (p_out == NULL) {
            printf("无");
        } else {
            while (p_out != NULL) {
                printf("<%d, %d> ", G->xList[p_out->tailvex].data, G->xList[p_out->headvex].data);
                p_out = p_out->hlink;
            }
        }

        // 输出入边（firstin + tlink）
        printf("\n  入边：");
        ArcNode *p_in = G->xList[i].firstin;
        if (p_in == NULL) {
            printf("无");
        } else {
            while (p_in != NULL) {
                printf("<%d, %d> ", G->xList[p_in->tailvex].data, G->xList[p_in->headvex].data);
                p_in = p_in->tlink;
            }
        }
        printf("\n");
    }
}

4. 扩展操作：统计顶点的出度/入度

// 统计单个顶点的出度和入度
void CountDegree(OLGraph *G, int v) {
    int idx = LocateVex(G, v);
    if (idx == -1) {
        printf("顶点%d不存在！\n", v);
        return;
    }

    // 出度：出边链表的长度
    int out_degree = 0;
    ArcNode *p_out = G->xList[idx].firstout;
    while (p_out != NULL) {
        out_degree++;
        p_out = p_out->hlink;
    }

    // 入度：入边链表的长度
    int in_degree = 0;
    ArcNode *p_in = G->xList[idx].firstin;
    while (p_in != NULL) {
        in_degree++;
        p_in = p_in->tlink;
    }

    printf("顶点%d的出度：%d，入度：%d\n", v, out_degree, in_degree);
}

5. 测试主函数

int main() {
    OLGraph G;
    InitOLGraph(&G);       // 初始化十字链表
    PrintOLGraph(&G);      // 遍历输出

    // 统计指定顶点的度
    int target;
    printf("\n请输入要统计度的顶点值：");
    scanf("%d", &target);
    CountDegree(&G, target);

    // 释放内存（可选，避免内存泄漏）
    // 思路：遍历所有边节点，逐个free
    for (int i = 0; i < G.vexnum; i++) {
        ArcNode *p = G.xList[i].firstout;
        while (p != NULL) {
            ArcNode *q = p;
            p = p->hlink;
            free(q);
        }
    }

    return 0;
}

6. 带权图扩展（仅修改核心代码）

若需存储带权有向图，仅需：

在ArcNode中新增weight字段；

初始化边时输入权重并赋值：

// 输入时新增权重
int v1, v2, w;
printf("请输入有向边<v1, v2>的起点、终点和权重：");
scanf("%d%d%d", &v1, &v2, &w);
p->weight = w;

遍历输出时补充权重：

printf("<%d, %d, %d> ", ..., p_out->weight);

4、关键特性分析

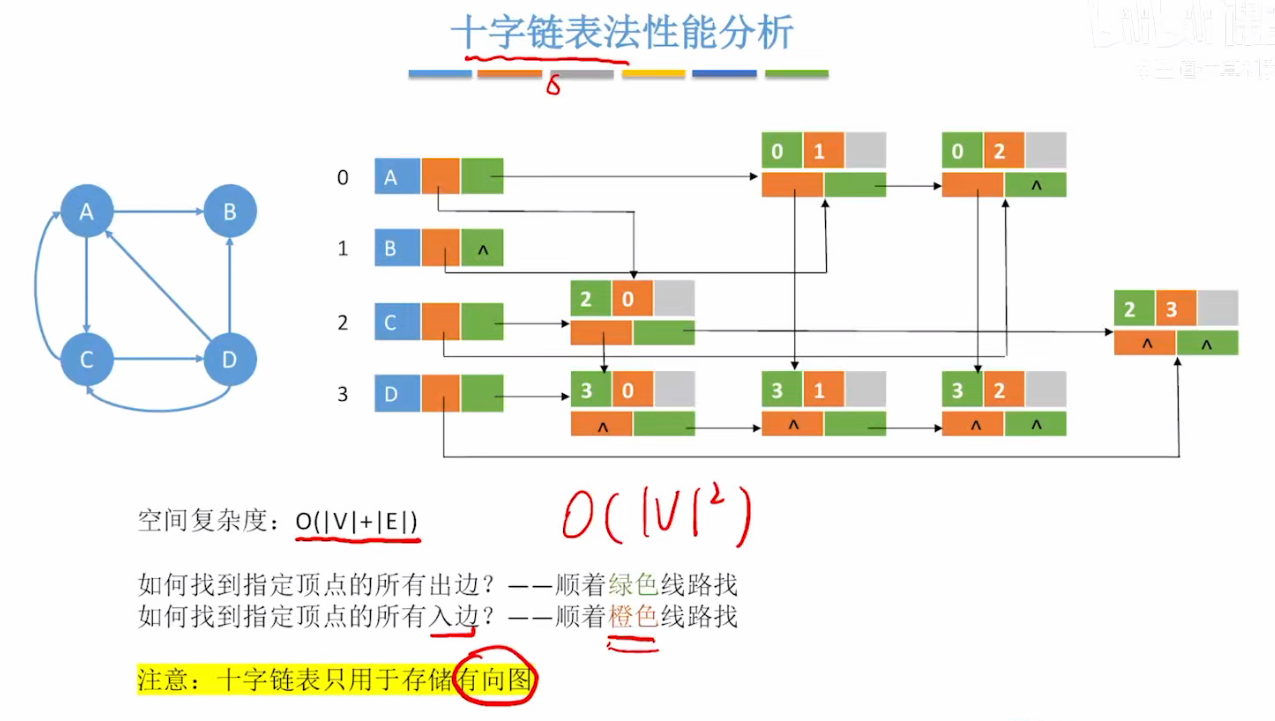
1. 空间复杂度

顶点表：O(n)（n为顶点数）；
边表：O(e)（e为边数，每条边仅存储一次）；
总空间复杂度：O(n + e)，与邻接表完全一致，无额外空间开销。

2. 时间复杂度

操作	时间复杂度	说明
查顶点的所有出边	O(出度)	直接遍历firstout + hlink
查顶点的所有入边	O(入度)	直接遍历firstin + tlink
统计出度/入度	O(出度/入度)	遍历对应链表
查找指定边<v1,v2>	O(出度(v1))	遍历v1的出边链表
图的遍历（DFS/BFS）	O(n + e)	与邻接表效率一致
新增边	O(1)	头插法直接插入出边/入边链表

3. 优缺点对比

优点	缺点
同时高效访问出边/入边	实现比单纯邻接表复杂（需维护两个链表）
空间效率与邻接表一致	查找指定边仍需遍历出边链表
适配有向图的各类操作	增删顶点需调整所有相关边的索引
支持带权图扩展	指针管理易出错（需注意内存泄漏）

5、工程应用场景

有向图的核心算法：如拓扑排序、关键路径（CPM）、有向无环图（DAG）的最短路径，需同时访问入边/出边；
编译器优化：存储程序的控制流图（CFG），分析指令的依赖关系（入边=前驱指令，出边=后继指令）；
网络路由：存储有向网络拓扑（如单向链路），同时统计入站/出站流量；
依赖分析：如项目管理中的任务依赖（A→B表示A依赖B），快速查某任务的前置依赖（入边）和后置任务（出边）。

6、与邻接表/逆邻接表的对比

存储方案	出边访问	入边访问	空间复杂度	适用场景
邻接表	高效	低效	O(n+e)	仅需频繁查出边的有向图
逆邻接表	低效	高效	O(n+e)	仅需频繁查入边的有向图
十字链表	高效	高效	O(n+e)	需同时查出入边的有向图

选择原则：

仅需处理出边（如单纯的DFS/BFS）→ 邻接表；
仅需处理入边（如统计入度）→ 逆邻接表；
需同时处理出边+入边（如拓扑排序、关键路径）→ 十字链表（最优选择）。

十字链表动态演示 Orthogonal List Demo

1、核心概念​

1. 定义​

2. 核心解决的问题​

3. 核心术语​

2、结构设计（核心）​

1. 顶点表节点结构​

2. 边表节点结构​

3. 十字链表整体结构​

4. 结构示意图（有向图示例）​

3、完整代码实现（C语言）​

1. 基础定义与辅助函数​

2. 核心操作：初始化十字链表​

3. 遍历操作：输出顶点的出边/入边​

4. 扩展操作：统计顶点的出度/入度​

5. 测试主函数​

6. 带权图扩展（仅修改核心代码）​

4、关键特性分析​

1. 空间复杂度​

2. 时间复杂度​

3. 优缺点对比​

5、工程应用场景​

6、与邻接表/逆邻接表的对比​

💬 留下你的问题或见解