七.广度优先遍历

1.代码

bool visited[MAX_VERTEX_NUM]; //访问标记数组

//广度优先遍历
void BFS(Graph G, int v) { //从顶点v出发, 广度优先遍历图G
    visit(v);             //访问初始顶点v
    visited[v] = TRUE;      //对v做已访问标记
    Enqueue(Q, v);         //顶点v入队列Q
    while (!isEmpty(Q)) {
        DeQueue(Q, v);     //顶点v出队列
        for (w = FirstNeighbor(G, v);w >= 0;w = NextNeighbor(G, v, w))
            //检测v所有邻接点
            if (!visited[w]) { //w为v的尚未访问的邻接顶点
                visit(w);     //访问顶点w
                visited[w] = TRUE;//对w做已访问标记
                EnQueue(Q, w); //顶点w入队列
            }//if
    }//while
}

BFS 演示
-
Start:?
逻辑结构 (Graph)
双击删除此连线双击删除此连线双击删除此连线双击删除此连线双击删除此连线双击删除此连线双击删除此连线1
2
3
4
5
6
C++ Code (BFS with Queue)
void BFS(Graph G, int start) {
    visited[start] = TRUE; Queue.push(start);
    while (!Queue.empty()) {
        u = Queue.pop(); // 取队头
        for (w = FirstAdj(u); w; w = NextAdj(u, w)) {
            if (!visited[w]) {
                visited[w] = TRUE; Queue.push(w);
            }
        }
    }
}
Queue Visualization (FIFO)Size: 0
Head (出队)
Tail (入队)
Queue Empty
Log (操作日志)
准备就绪。 请选择 Start (起始节点)，然后点击 "开始遍历"。
* BFS 使用队列 (Queue) 实现层序遍历。

2.图解代码

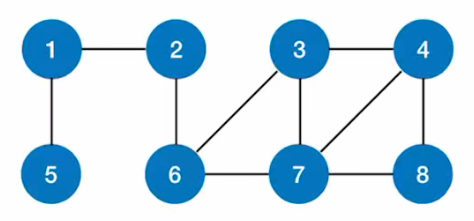
如果我们从2号顶点出发广度优先遍历整个图;

首先,访问2号结点: visit(v);
然后, 将2号结点对应的数组设为 true;表示已经被访问过了: visited[v] = TRUE;
再将2号顶点入队;指针指向队头元素:2 Enqueue(Q, v);
如果队头元素不空, 那我们就让队头顶点出队 : 2出队 DeQueue(Q, v);
然后检查2所有的邻接点, 又因为1和6都没有被访问过 : visited[1, 6] = false;
所以正常访问 1, 6 顶点;再标记为 true;visit(w); visited[w] = TRUE;
然后将顶点入队,且放在队尾 EnQueue(Q, w);

然后再进行下一次循环:

因为此时队列为非空的,所以让1号元素出队:
此时,又到了 for循环 ,与1号相邻的有2号,5号;
因为2号的 visit 值为 True,不满足条件,所以2号结点不会再进行其他处理
处理5号顶点,标记为True;并入队尾

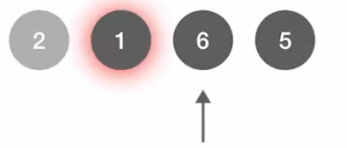
接下来处理6号顶点:

6号顶点连接3,7;且这两个顶点 visit 都为 False;
所以3号,7号入队尾,且标记为 True;

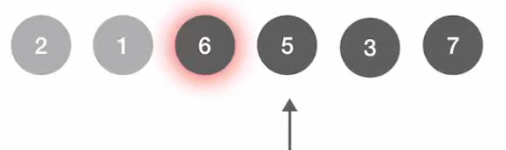
同时,5号结点出队 接下来处理5号顶点:

5号顶点只连接了1号,1号为 True;所以5号不用处理了

所以,接下来3号顶点出队:

3号顶点连接4,7;7号 visit 值为 True;所以4号入队

最后,处理7号顶点:

7号顶点连接4,8;4号 visit 值为 True;所以8号入队

到这里就完成了对这张图的广度优先遍历

3.特殊情况

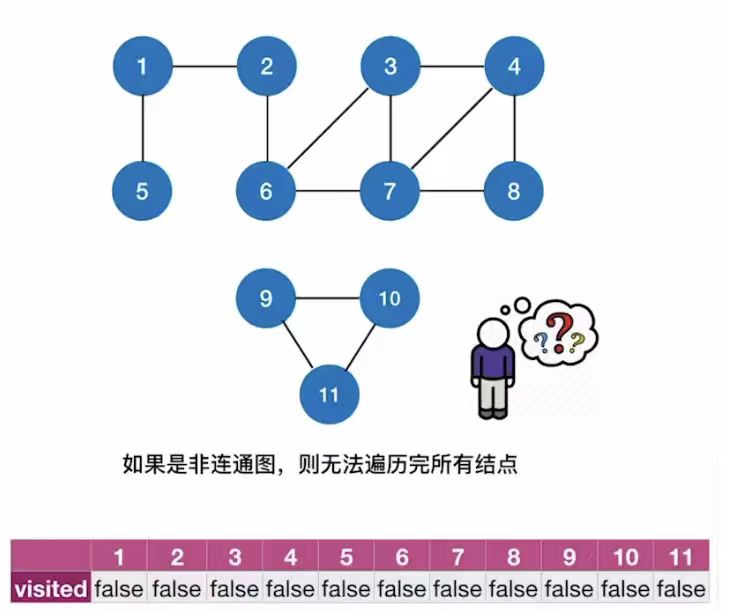
如上图所示: 如果是非连通图,则无法遍历完所有结点;

首先,将 visit 数组全部设为 False,进行初始化处理;
然后,初始化一个辅助队列;
进行一个 for循环;扫描第一个为False的元素;
然后就会从该顶点出发,调用BFS函数

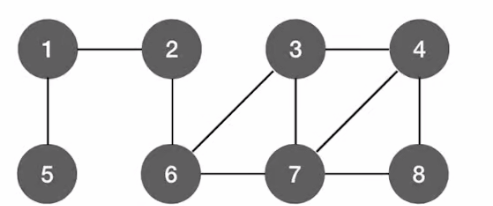
如上图所示:

第一次调用BFS函数访问完1-8的结点;
此时1-8结点的visit值为True;
此时再进行BFSTraverse函数中的for循环,遍历到9号元素为False;
再调用BFS函数完成广度优先遍历

bool visited[MAX_VERTEX_NUM]; //访问标记数组
void BFSTraverse(Graph G) { //对图G进行广度优先遍历
    for (i = 0;i < G.vexnum;++i)
        visited[i] = FALSE;     //访问标记数组初始化
    InitQueue(Q);             //初始化辅助队列Q
    for (i = 0;i < G.vexnum;++i)   //从0号顶点开始遍历
        if (!visited[i])       //对每个连通分量调用一次BFS
            BFS(G, i);         //vi未访问过，从vi开始BFS
}
//广度优先遍历
void BFS(Graph G, int v) { //从顶点v出发, 广度优先遍历图G
    visit(v);             //访问初始顶点v
    visited[v] = TRUE;      //对v做已访问标记
    Enqueue(Q, v);         //顶点v入队列Q
    while (!isEmpty(Q)) {
        DeQueue(Q, v);     //顶点v出队列
        for (w = FirstNeighbor(G, v);w >= 0;w = NextNeighbor(G, v, w))
            //检测v所有邻接点
            if (!visited[w]) { //w为v的尚未访问的邻接顶点
                visit(w);     //访问顶点w
                visited[w] = TRUE;//对w做已访问标记
                EnQueue(Q, w); //顶点w入队列
            }//if
    }//while
}

4.复杂度

广度优先遍历（BFS）的时间复杂度和空间复杂度取决于图的存储方式和图的结构，以下是详细分析：

(1)、时间复杂度

BFS的时间开销主要来自「访问所有顶点」和「遍历所有边」，与图的存储方式强相关：

邻接表存储：遍历每个顶点的邻接链表，总时间为「顶点数 ( n )」+「边数 ( e )」，时间复杂度为 ( \boldsymbol{O(n + e)} )。
邻接矩阵存储：需遍历每个顶点的整行（检查是否有边），总时间为 ( n^2 )，时间复杂度为 ( \boldsymbol{O(n^2)} )。

(2)、空间复杂度

BFS的空间开销主要来自「辅助队列」和「访问标记数组」：

访问标记数组：大小为 ( n )（顶点数），空间复杂度为 ( O(n) )。
辅助队列：队列的最大长度取决于「图的最大层顶点数」（最坏情况是稠密图的某层包含所有顶点），最坏空间复杂度为 ( O(n) )。

因此，BFS的总空间复杂度为 ( \boldsymbol{O(n)} )（无论存储方式）。

(3)、总结

存储方式	时间复杂度	空间复杂度
邻接表	( O(n+e) )	( O(n) )
邻接矩阵	( O(n^2) )	( O(n) )

5.广度最小生成树

生成树演示
-
Root:?
原始图 (可编辑/拖拽)
双击删除双击删除双击删除双击删除双击删除双击删除双击删除双击删除A
B
C
D
E
F
G
结果：BFS 生成树
BFS 生成树
请编辑图结构或直接点击生成

6.广度优先生成树和森林

自定义图的遍历与森林生成

在这里，你可以自由绘制一个图（甚至是非连通图），然后观察 BFS 和 DFS 算法是如何运行的。

交互说明

添加节点：点击上方“+ 节点”按钮。
连线：点击一个节点（变金），再点击另一个节点。
移动：按住节点拖拽。
删除：双击节点。
切换算法：左上角选择 BFS 或 DFS。

💡 点击两个节点连线，拖拽移动，双击删除

辅助队列 (Queue)

Empty

Front ↑ ... Rear ↓

准备就绪

实验建议

试着画两个互不相连的三角形，然后点击“开始生成森林”，观察算法是如何自动跳跃到第二个连通分量的。

广度优先搜索 (BFS) 类似于树的层序遍历。如果我们将 BFS 遍历过程中经过的边记录下来，就会得到一棵广度优先生成树。

动态演示

左侧 (Graph)：原始图结构。你可以拖动节点，或添加新的节点/连线。
右侧 (Tree)：随着遍历进行，自动生成的树形结构。注意观察树的层级关系。
下方 (Queue)：辅助队列的实时状态，理解 BFS "先进先出" 的特性。

原始图结构 (Graph)

广度优先生成树 (BFS Tree)

点击左上角「开始 BFS」生成树

Queue:

Empty

💬 准备就绪

生成树核心性质

最短路径：在无权图中，BFS 生成树中根节点到任意节点的路径，就是原图中该两点间的最短路径（边数最少）。
非树边：原图中的非树边（如演示中的 B-C 边），在生成树中连接的必然是同一层或相邻层的节点。

1.代码​

BFS 演示

2.图解代码​

3.特殊情况​

4.复杂度​

(1)、时间复杂度​

(2)、空间复杂度​

(3)、总结​

5.广度最小生成树​

生成树演示

6.广度优先生成树和森林​

自定义图的遍历与森林生成​

交互说明​