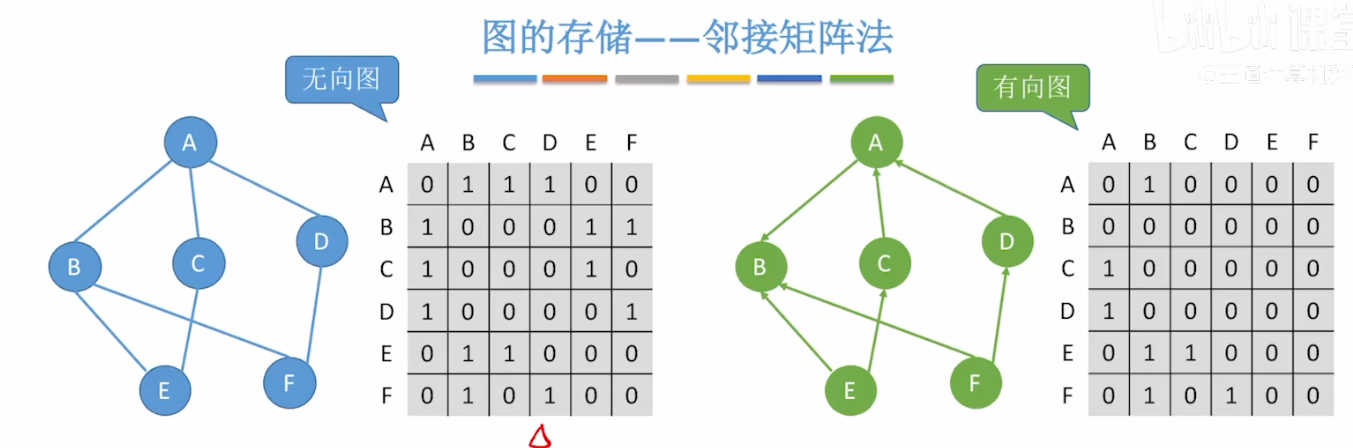
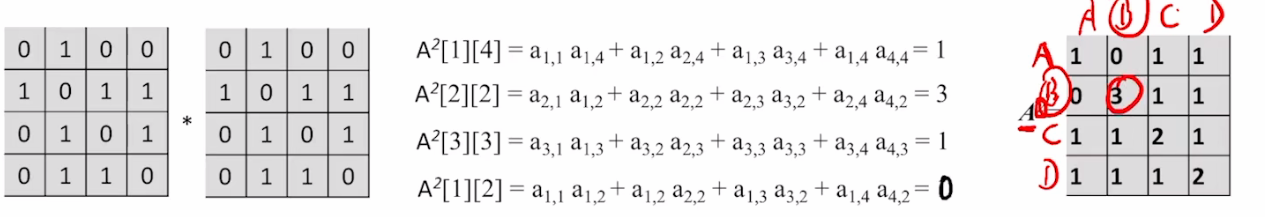二.邻接矩阵法
可切换有向图/无向图
邻接矩阵演示
1.图的存储--邻接矩阵法
#define MaxVertexNum 100 //顶点数目的最大值
typedef struct {
char Vex[MaxVertexNum]; //顶点表
int Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, arcnum; //图的当前顶点数和边数,弧数
};
第i个结点的度 = 第i行(或第i列)的非零元素个数
第i个结点的出度 = 第i行的非零元素个数
第i个结点的入度 = 第i列的非零元素个数
第i个结点的度 = 第i行、第i列的非零元素个数之和
邻接矩阵法求顶点的度/出度/入度的时间复杂度为 O(|V|)
2.邻接矩阵法存储带权图(网)
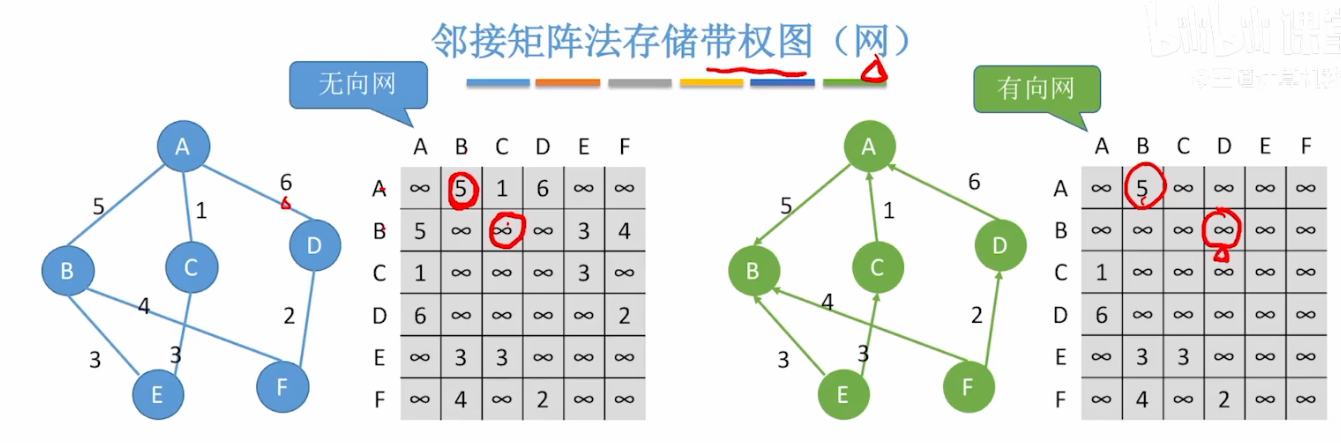
#define MaxVertexNum 100 // 顶点数目的最大值
#define INFINITY 最大的int值 // 宏定义常量“无穷”
typedef char VertexType; // 顶点的数据类型
typedef int EdgeType; // 带权图中边上权值的数据类型
typedef struct {
VertexType Vex[MaxVertexNum]; // 顶点
EdgeType Edge[MaxVertexNum][MaxVertexNum]; // 边的权
int vexnum, arcnum; // 图的当前顶点数和弧数
} MGraph;
3.邻接矩阵法的性能分析
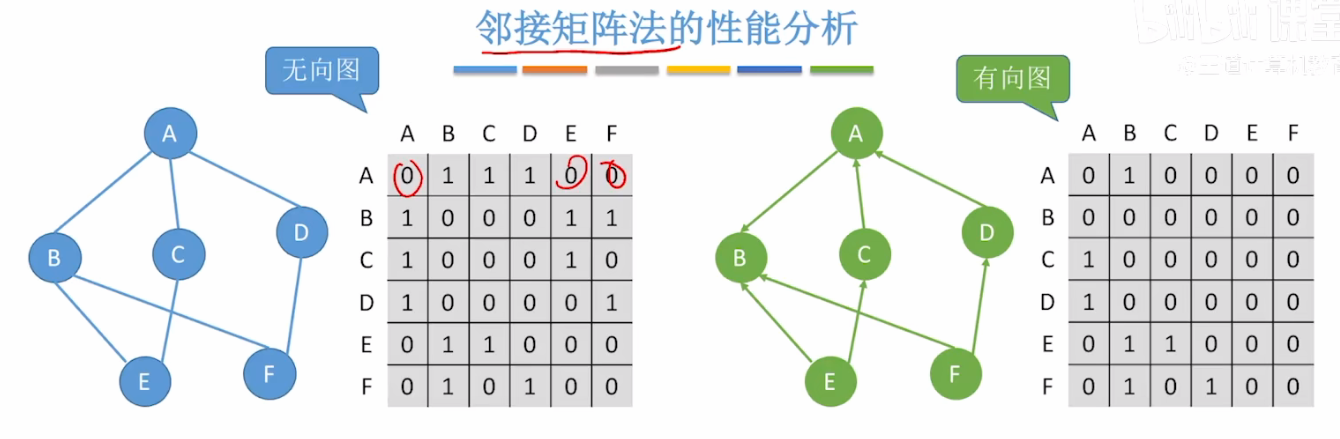 空间复杂度:O(|V|²) —— 只和顶点数相关,和实际的边数无关
适合用于存储
空间复杂度:O(|V|²) —— 只和顶点数相关,和实际的边数无关
适合用于存储稠密图
无向图的邻接矩阵是对称矩阵,可以压缩存储(只存储上三角区 / 下三角区
4.邻接矩阵法的性质
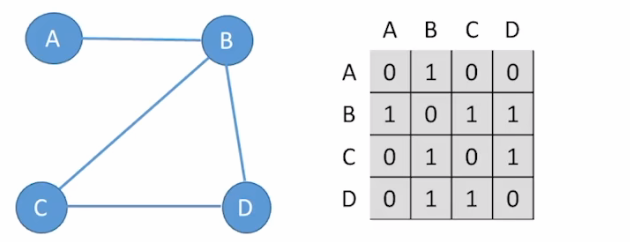 设图 G 的邻接矩阵为 A(矩阵元素为 0/1),
则 Aⁿ 的元素 Aⁿ[i][j] 等于由顶点 i 到顶点 j 的长度为 n 的路径的数目。
设图 G 的邻接矩阵为 A(矩阵元素为 0/1),
则 Aⁿ 的元素 Aⁿ[i][j] 等于由顶点 i 到顶点 j 的长度为 n 的路径的数目。
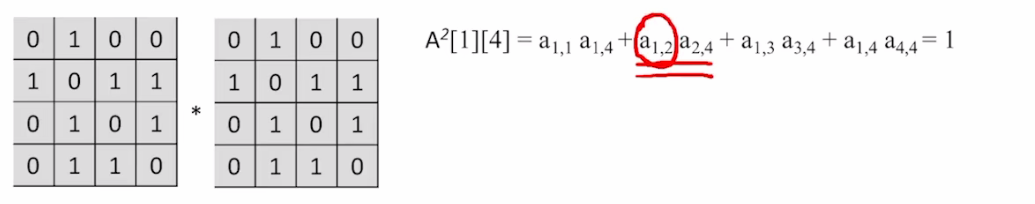 如上图所示:
如上图所示:
A2[1][4]表示的为:从顶点A到顶点D的长度为2的路径的数目
- a[1,2]元素对应的是第一行第二列的元素即A->B,为1,即
路径为1; - a[2,4]元素对应的是第二行第四列的元素即B->D,为1,即
路径为1; 所以a[1,2]*a[2,4]=1; 同理: - a[1,3]元素对应的是第一行第二列的元素即A->C,为0,即
路径为0; - a[3,4]元素对应的是第二行第四列的元素即C->D,为1,即
路径为1; 所以a[1,3]*a[3,4]=0;