跳到主要内容

五.邻接多重表存储无向图

Img Img

邻接多重表演示 Adjacency Multilist

—
逻辑无向图 (Undirected Graph)
A
B
C
D
E
邻接多重表存储 (Adjacency Multilist)
^^^^^
A
firstedge
B
firstedge
C
firstedge
D
firstedge
E
firstedge
i:A
j:B
iLink
jLink
i:A
j:C
iLink
jLink
i:B
j:C
iLink
jLink
i:C
j:D
iLink
jLink
i:C
j:E
iLink
jLink
── iLink (连接所有与 i 相关的边)
── jLink (连接所有与 j 相关的边)
C++ Struct Definition
struct EBox {
  int ivex, jvex; // 该边依附的两个顶点
  EBox *ilink;    // iLink: 依附于 ivex 的下一条边
  EBox *jlink;    // jLink: 依附于 jvex 的下一条边
  // InfoType info; // 权值等
};

struct VexBox {
  VertexType data;
  EBox *firstedge; // 指向第一条依附该顶点的边
};
系统日志 (System Logs)
初始化无向图与邻接多重表...

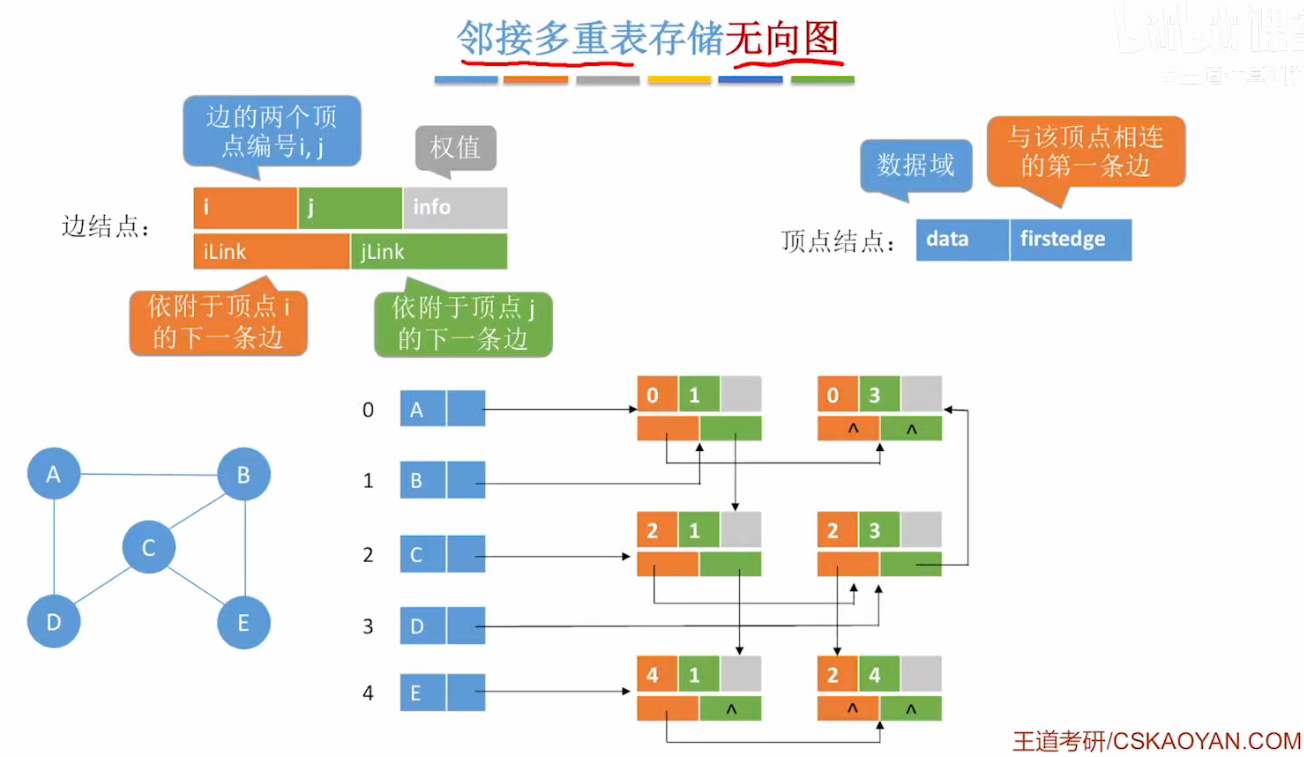
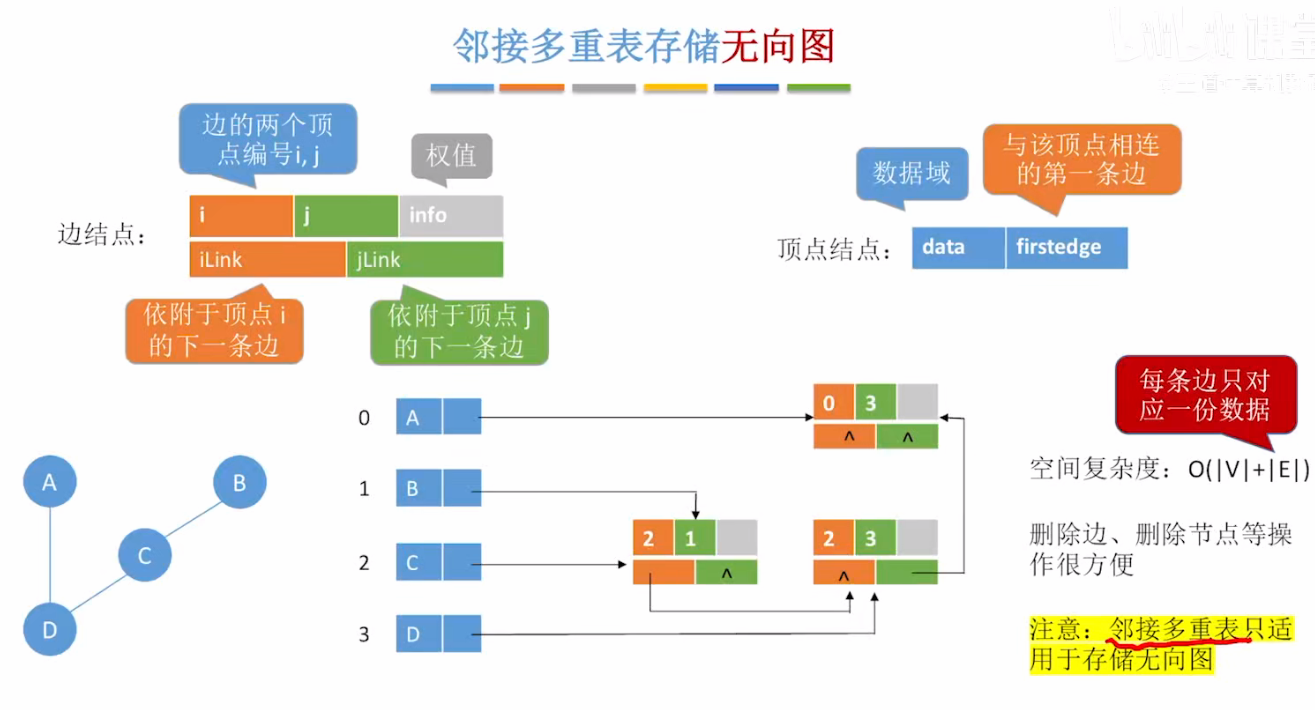
1、邻接多重表是什么？​

邻接多重表（Adjacency Multilist） 是一种专门用于存储无向图的链式存储结构。

它解决了邻接表存储无向图时同一条边要存储两次的问题。

2、邻接表的痛点（邻接多重表要解决的问题）​

在邻接表中，无向图的每条边 (A, B) 会存储两次：

  • 一次在 A 的边表中：(A) → [B] → ...
  • 一次在 B 的边表中：(B) → [A] → ...

❌ 缺点：

  • 冗余存储：同一条边存两次，浪费空间。
  • 操作麻烦：删除边时，要同时删除两个结点，效率低。

3、邻接多重表的核心思想​

每条边只存储一次，但让它同时出现在两个顶点的链表中。

4、邻接多重表的存储结构（图解）​

✅ 1. 顶点结构（顶点表）

每个顶点用一个结构体表示： | data | firstedge| | :-- | :-- | | 顶点信息 | 指向第一条依附于该顶点的边 | data firstedge 顶点信息 指向第一条依附于该顶点的边

✅ 2. 边结构（边结点）

每条边用一个结构体表示，同时挂在两个顶点的链表中：

ivexjvexilink
边的一个顶点编号另一个顶点编号指向下一条依附于 ivex 的边

5、邻接多重表的图示（文字版）​

假设无向图如下：

A
|\
B C

边为：(A, B) 和 (A, C)

✅ 邻接多重表结构：

顶点表：
[A] → (A,B) → (A,C) → NULL
[B] → (A,B) → NULL
[C] → (A,C) → NULL

✅ 边结点详情：

  • 边 (A,B)：

    • ivex = A, jvex = B
    • ilink 指向 (A,C)
    • jlink 指向 NULL

  • 边 (A,C)：

    • ivex = A, jvex = C
    • ilink 指向 NULL
    • jlink 指向 NULL

🔍 问题重述：

为什么边 (A,B) 的 ilink 会指向 (A,C)？

✅ 先明确两个概念：

字段含义
ivex这条边的“第一个”顶点编号（人为指定，无先后意义）
ilink指向下一条同样以 ivex 为端点的边

✅ 回到例子：

我们有无向图：

A
|\
B C

边为：(A,B) 和 (A,C)

✅ 边结点设计（人为设定）：

边ivexjvex
(A,B)AB
(A,C)AC

✅ 现在看 ilink 的含义：

  • ilink 是：“下一条同样以 A 为端点的边”

所以：

  • 边 (A,B) 的 ilink 指向 (A,C)，因为下一条以 A 为端点的边就是 (A,C)
  • 边 (A,C) 的 ilink 指向 NULL，因为后面没有以 A 为端点的边了

✅ 形象理解（类比）：

可以把 ilink 想象成：“A 的边链表”，就像邻接表里 A 的边表一样，只不过在邻接多重表里，这些边是共享的。

✅ 再画一次结构（A 的视角）：

A 的边链表：
(A,B) → (A,C) → NULL
   ↑        ↑
 ilink    ilink

✅ 总结一句话：

ilink 指向的是“下一条同样以 ivex 为端点的边”，所以 (A,B) 的 ilink 指向 (A,C)，因为它们都以 A 为端点。

6、邻接多重表的优点​

优点说明
✅ 无冗余每条边只存一次，节省空间
✅ 删除边快只需删除一个边结点，效率 O(1)
✅ 标记边方便访问过的边只需标记一次

7、邻接多重表 vs 邻接表​

特性邻接表邻接多重表
存储边数2 × 边数边数
删除边效率慢（需删两次）快（删一次）
空间效率低（冗余）高
适用图类型有向/无向仅无向图

8、总结​

邻接多重表就是“让一条边同时挂在两个顶点的链表中”，解决邻接表冗余存储和删边慢的问题，是专门为无向图优化的链式存储结构。 Img

💬 留下你的问题或见解