一.图的基本概念
1、图的定义
图 G 由顶点集 V 和边集 E 组成,记作:
G = (V, E)
- |V|:顶点个数,称为图的阶
- |E|:边的条数
⚠️ 注意:
- 线性表可以为空,树可以为空,但 图不可以为空图,即 V 必须是非空集合
2、图的分类
- 无向图 vs 有向图
| 类型 | 边的表示 | 特点描述 | |
|---|---|---|---|
| 无向图 | (v, w) | 边无方向,(v, w) = (w, v) | |
| 有向图 | <v, w> | 边有方向,<v, w> ≠ <w, v>,v 为弧尾,w 为弧头 |
3、简单图与多重图
| 类型 | 定义说明 | |
|---|---|---|
| 简单图 | 无重复边,无边连接到自身 | |
| 多重图 | 允许两个顶点间有多条边,允许自环 |
数据结构课程中仅讨论简单图
4、顶点的度
无向图:
- 度 TD(v):与顶点 v 相连的边的数量
- 所有顶点度之和:
有向图:
入度 ID(v):指向顶点 v 的边的数量
出度 OD(v):从顶点 v 出发的边的数量
总度:
TD(v) = ID(v) + OD(v)
所有顶点入度之和 = 出度之和 = |E|
5、路径相关概念
- 路径:顶点序列,相邻顶点之间有边
- 简单路径:路径中顶点不重复
- 简单回路:起点和终点相同,其余顶点不重复
- 点到点距离:从 u 到 v 的最短路径长度(若无路径,距离为 ∞)
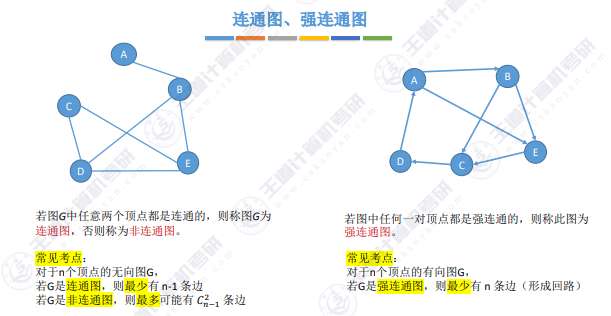
6、连通性
无向图:
- 连通图:任意两个顶点之间都有路径
- 非连通图:存在不连通的顶点
- 连通分量:极大连通子图
有向图:
- 强连通图:任意两个顶点 u 和 v 之间都有双向路径
- 强连通分量:极大强连通子图
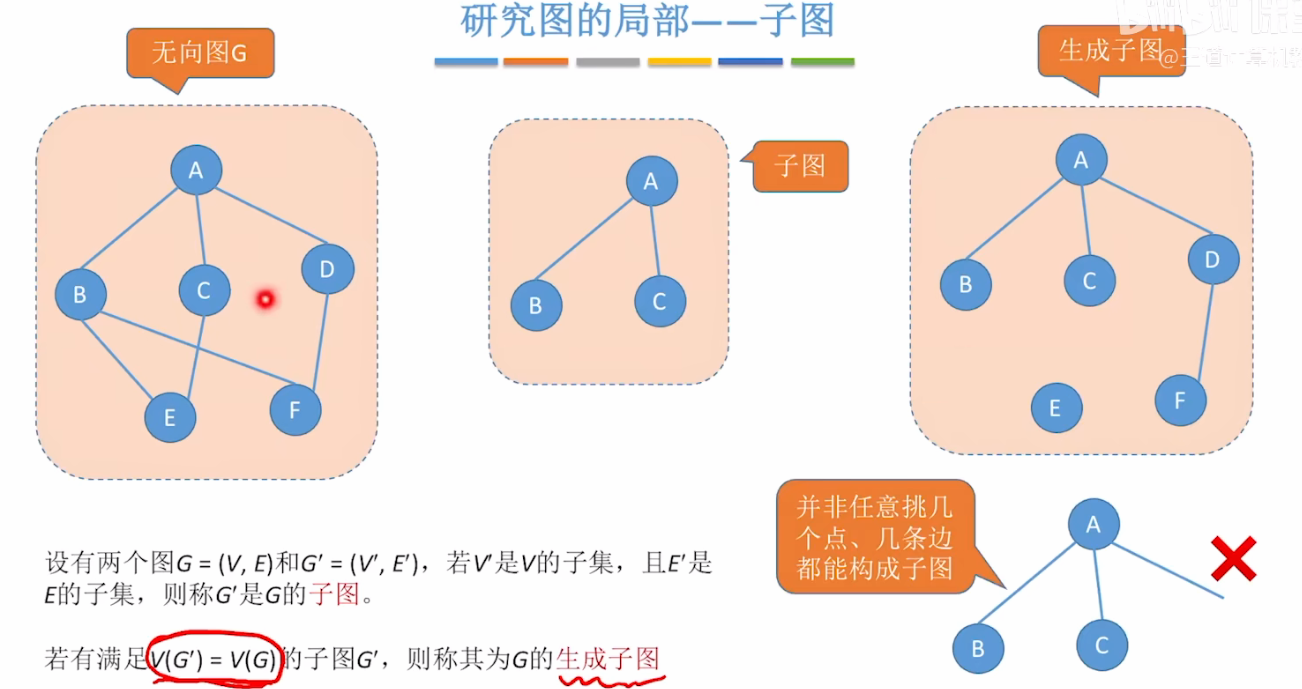
7、子图与生成图
- 子图:G' = (V', E'),其中 V' ⊆ V,E' ⊆ E
- 生成子图:V' = V,E' ⊆ E
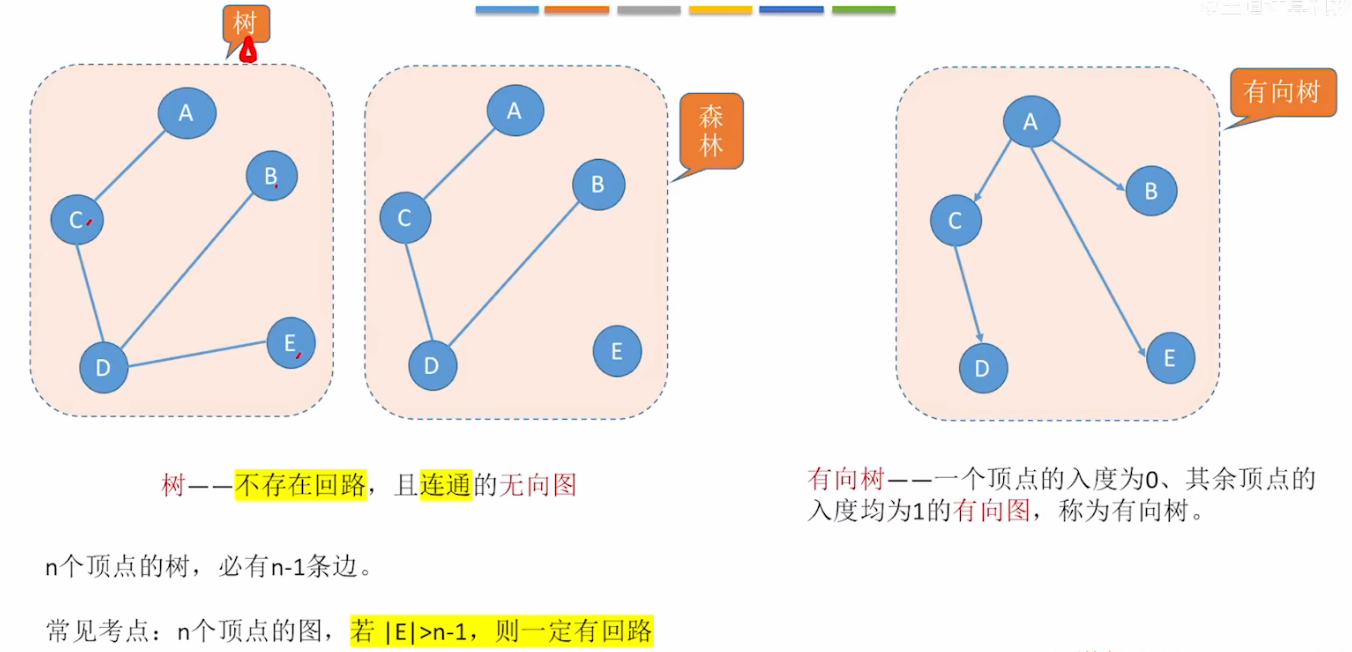
- 生成树:连通图的极小连通子图,包含所有顶点,边数为 n-1
- 生成森林:非连通图中各连通分量的生成树集合
8、带权图(网)
- 边的权:边所附带的数值(如距离、费用等)
- 带权图/网:边带权值的图
- 带权路径长度:路径上所有边的权值之和
9、特殊图形态
| 类型 | 特点描述 | |
|---|---|---|
| 完全图 | 任意两个顶点之间都有边(无向)或双向弧(有向) | |
| 稠密图 | 边数较多,通常 | |
| 稀疏图 | 边数较少,通常 | |
| 树 | 无向连通图,无回路,边数为 n-1 | |
| 有向树 | 有向图中,一个顶点入度为 0,其余顶点入度为 1 |
10、常见考点总结
无向图:
- 所有顶点度之和 = 2|E|
- 连通图最少有 n-1 条边
- 若 |E| > n-1,则图中必有回路
- 非连通图最多有 C(n-1, 2) 条边
- 完全图有 n(n-1)/2 条边
有向图:
- 所有顶点出度之和 = 入度之和 = |E|
- 所有顶点度之和 = 2|E|
- 强连通图最少有 n 条边(形成回路)
- 完全图有 n(n-1) 条边
