三.邻接表法

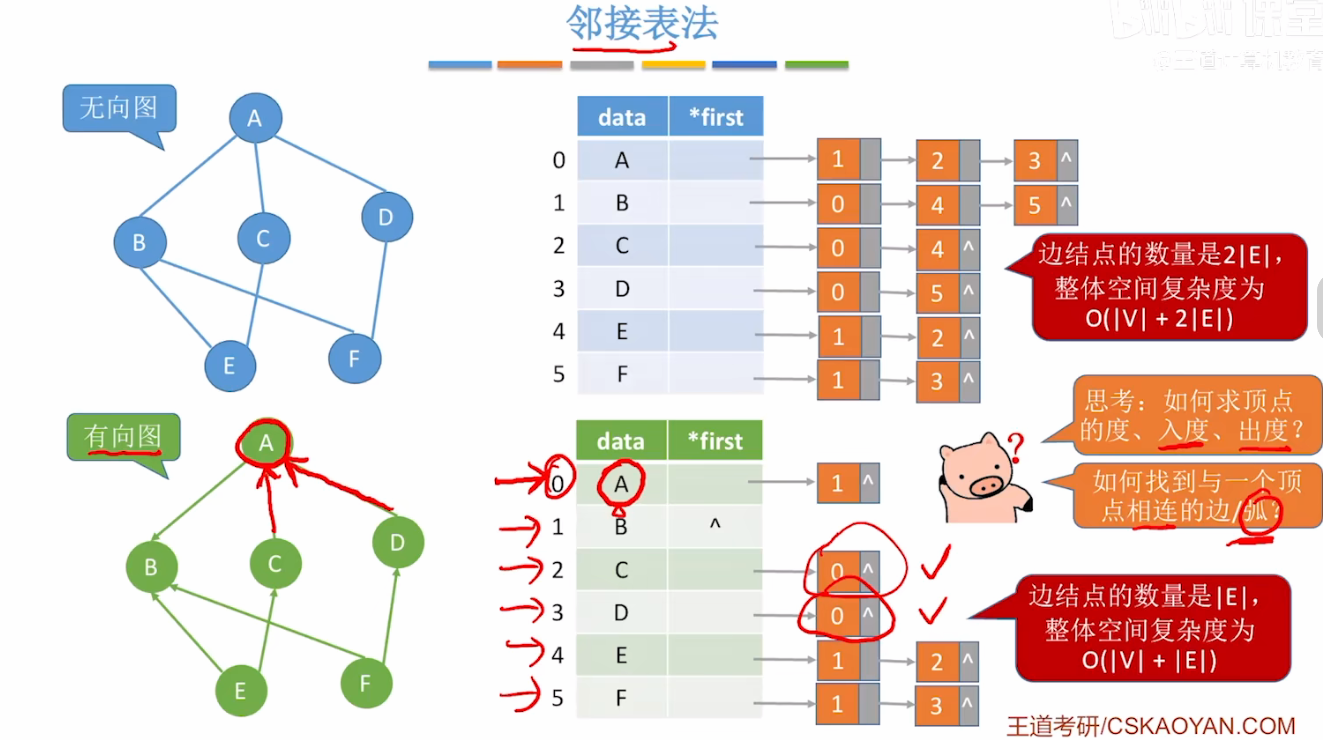
邻接表演示

ABCD→ABCD

逻辑结构 (Directed Graph)

A

B

C

D

存储结构 (Array + Linked Lists)

A

first

B

C

B

first

C

C

first

D

D

first

A

邻接表法（Adjacency List）知识点全解析 邻接表法是图的核心存储方式之一，与邻接矩阵法并列，因空间效率高、适配稀疏图等特点，成为工程中最常用的图存储方案。本文从核心概念、结构设计、代码实现到优劣分析，全面讲解邻接表法的知识点。

1、核心概念

1. 定义

邻接表法通过「数组 + 链表」的组合结构存储图：

• 顶点表：用一维数组存储图中所有顶点的基本信息（如顶点值、索引）；
• 边表（邻接链表）：数组中每个顶点对应一条链表，链表节点存储该顶点的邻接点索引及边的附加信息（如权重、方向）。

2. 适用场景

• 稀疏图（顶点多、边少）：空间效率远高于邻接矩阵（邻接矩阵会浪费大量空位置）；
• 需频繁遍历邻接点的场景（如图的遍历、最短路径算法）；
• 动态增删顶点/边的场景（链表结构支持高效插入删除）。

3. 核心术语

术语	说明
顶点表节点	存储顶点值 + 指向该顶点第一条邻接边的指针
边表节点	存储邻接点的索引 + 指向下一个邻接边的指针（若为带权图，新增权重字段）
出度/入度	有向图中，顶点的出度 = 对应链表长度；入度需遍历所有链表统计

2、结构设计（无向图 vs 有向图 vs 带权图）

1. 无向图的邻接表

无向图中，边 (v1, v2) 会被存储两次：

• v1 的邻接链表中添加 v2；
• v2 的邻接链表中添加 v1。

示例：无向图 0-1-2，0-2 的邻接表结构：

顶点表（数组）：
索引 0 → 顶点值 0 → 边表：1 → 2 → NULL
索引 1 → 顶点值 1 → 边表：0 → 2 → NULL
索引 2 → 顶点值 2 → 边表：0 → 1 → NULL

2. 有向图的邻接表

有向图中，边 <v1, v2> 仅存储一次：

• 仅在 v1 的邻接链表中添加 v2（表示从 v1 指向 v2）。

示例：有向图 0→1，1→2，0→2 的邻接表结构：

顶点表（数组）：
索引 0 → 顶点值 0 → 边表：1 → 2 → NULL
索引 1 → 顶点值 1 → 边表：2 → NULL
索引 2 → 顶点值 2 → 边表：NULL

3. 带权图的邻接表

仅需在边表节点中新增「权重」字段，其余结构与无向/有向图一致。

示例：带权无向图 0-1(权重5)，1-2(权重3) 的邻接表结构：

顶点表（数组）：
索引 0 → 顶点值 0 → 边表：(邻接点1, 权重5) → NULL
索引 1 → 顶点值 1 → 边表：(邻接点0, 权重5) → (邻接点2, 权重3) → NULL
索引 2 → 顶点值 2 → 边表：(邻接点1, 权重3) → NULL

3、完整代码实现（C语言）

1. 基础结构定义（无向图）

#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX_NUM 100  // 最大顶点数

// 边表节点（存储邻接点索引 + 下一个边节点指针）
typedef struct ArcNode {
    int adjvex;               // 邻接点在顶点表中的索引
    struct ArcNode *nextarc;  // 指向下一个邻接边节点
} ArcNode;

// 顶点表节点（存储顶点值 + 指向第一条邻接边的指针）
typedef struct VNode {
    int data;                 // 顶点值（可替换为char/自定义类型）
    ArcNode *firstarc;        // 指向该顶点的第一条邻接边
} VNode;

// 邻接表结构（顶点表数组 + 顶点数 + 边数）
typedef struct {
    VNode adjList[MAX_VERTEX_NUM];
    int vexnum, arcnum;       // 顶点数、边数
} ALGraph;

2. 核心操作实现

（1）初始化图

// 查找顶点值对应的索引（辅助函数）
int LocateVex(ALGraph *G, int v) {
    for (int i = 0; i < G->vexnum; i++) {
        if (G->adjList[i].data == v) {
            return i;
        }
    }
    return -1;  // 顶点不存在
}

// 初始化邻接表（无向图）
void InitGraph(ALGraph *G) {
    printf("请输入顶点数和边数：");
    scanf("%d%d", &G->vexnum, &G->arcnum);

    // 1. 初始化顶点表
    for (int i = 0; i < G->vexnum; i++) {
        printf("请输入顶点%d的值：", i);
        scanf("%d", &G->adjList[i].data);
        G->adjList[i].firstarc = NULL;  // 初始无邻接边
    }

    // 2. 初始化边表（无向图，每条边存两次）
    for (int k = 0; k < G->arcnum; k++) {
        int v1, v2;
        printf("请输入边(v1, v2)的两个顶点值：");
        scanf("%d%d", &v1, &v2);

        // 查找顶点对应的索引
        int i = LocateVex(G, v1);
        int j = LocateVex(G, v2);
        if (i == -1 || j == -1) {
            printf("顶点不存在，跳过该边！\n");
            k--;  // 重新输入该边
            continue;
        }

        // ① 为v1添加邻接点v2（头插法，效率更高）
        ArcNode *p1 = (ArcNode *)malloc(sizeof(ArcNode));
        p1->adjvex = j;
        p1->nextarc = G->adjList[i].firstarc;
        G->adjList[i].firstarc = p1;

        // ② 为v2添加邻接点v1（无向图特性）
        ArcNode *p2 = (ArcNode *)malloc(sizeof(ArcNode));
        p2->adjvex = i;
        p2->nextarc = G->adjList[j].firstarc;
        G->adjList[j].firstarc = p2;
    }
}

（2）遍历邻接表（输出所有顶点和邻接点）

void PrintGraph(ALGraph *G) {
    printf("\n邻接表遍历结果：\n");
    for (int i = 0; i < G->vexnum; i++) {
        printf("顶点%d（值：%d）的邻接点：", i, G->adjList[i].data);
        ArcNode *p = G->adjList[i].firstarc;
        while (p != NULL) {
            printf("%d ", G->adjList[p->adjvex].data);
            p = p->nextarc;
        }
        printf("\n");
    }
}

（3）深度优先遍历（DFS）

// 访问标记数组（全局变量，初始为0）
int visited[MAX_VERTEX_NUM] = {0};

// 访问顶点（可自定义逻辑，此处仅打印）
void Visit(int v) {
    printf("%d ", v);
}

// 深度优先遍历（从顶点v出发）
void DFS(ALGraph *G, int v) {
    Visit(G->adjList[v].data);  // 访问当前顶点
    visited[v] = 1;             // 标记为已访问

    // 遍历所有邻接点
    ArcNode *p = G->adjList[v].firstarc;
    while (p != NULL) {
        int w = p->adjvex;      // 邻接点索引
        if (!visited[w]) {      // 未访问则递归
            DFS(G, w);
        }
        p = p->nextarc;
    }
}

// 遍历整个图（处理非连通图）
void DFSTraverse(ALGraph *G) {
    printf("\n深度优先遍历结果：");
    // 重置访问标记
    for (int i = 0; i < G->vexnum; i++) {
        visited[i] = 0;
    }
    // 对未访问的顶点执行DFS
    for (int i = 0; i < G->vexnum; i++) {
        if (!visited[i]) {
            DFS(G, i);
        }
    }
    printf("\n");
}

（4）测试主函数

int main() {
    ALGraph G;
    InitGraph(&G);    // 初始化图
    PrintGraph(&G);   // 输出邻接表
    DFSTraverse(&G);  // 深度优先遍历

    // 释放内存（可选，避免内存泄漏）
    for (int i = 0; i < G.vexnum; i++) {
        ArcNode *p = G->adjList[i].firstarc;
        while (p != NULL) {
            ArcNode *q = p;
            p = p->nextarc;
            free(q);
        }
    }
    return 0;
}

3. 带权图的扩展（仅修改边表节点）

若需存储带权图，仅需修改边表节点结构，核心逻辑不变：

// 带权图的边表节点
typedef struct ArcNode {
    int adjvex;               // 邻接点索引
    int weight;               // 边的权重
    struct ArcNode *nextarc;  // 下一个边节点
} ArcNode;

// 初始化边表时新增权重输入
printf("请输入边(v1, v2)的两个顶点值和权重：");
scanf("%d%d%d", &v1, &v2, &weight);
p1->weight = weight;
p2->weight = weight;

4、关键特性分析

1. 空间复杂度

• 顶点表：O(n)（n 为顶点数）；
• 边表：无向图 O(2e)，有向图 O(e)（e 为边数）；
• 总空间复杂度：O(n + e)（稀疏图下远优于邻接矩阵的 O(n²)）。

2. 时间复杂度

操作	时间复杂度	说明
查找顶点的邻接点	O(度(v))	度(v)为顶点v的邻接边数
查找任意边 (v1,v2)	O(度(v1))	需遍历v1的邻接链表
图的遍历（DFS/BFS）	O(n + e)	访问所有顶点和边
增删边	O(1)	头插法直接插入，无需遍历
增删顶点	O(n + e)	需调整顶点表索引，并重排邻接链表

3. 优缺点对比

优点	缺点
空间效率高（适配稀疏图）	查找任意边效率低（需遍历链表）
遍历邻接点速度快	有向图统计入度需遍历所有链表
动态增删边/顶点更灵活	实现比邻接矩阵复杂（需处理链表指针）

5、工程应用场景

1. 社交网络：存储用户（顶点）和好友关系（边），快速查询某用户的所有好友；
2. 路由算法：存储网络节点（顶点）和链路（边），实现最短路径计算；
3. 编译器：存储语法树/依赖图，分析代码依赖关系；
4. 游戏开发：存储游戏场景中的角色（顶点）和交互关系（边），实现AI路径规划。

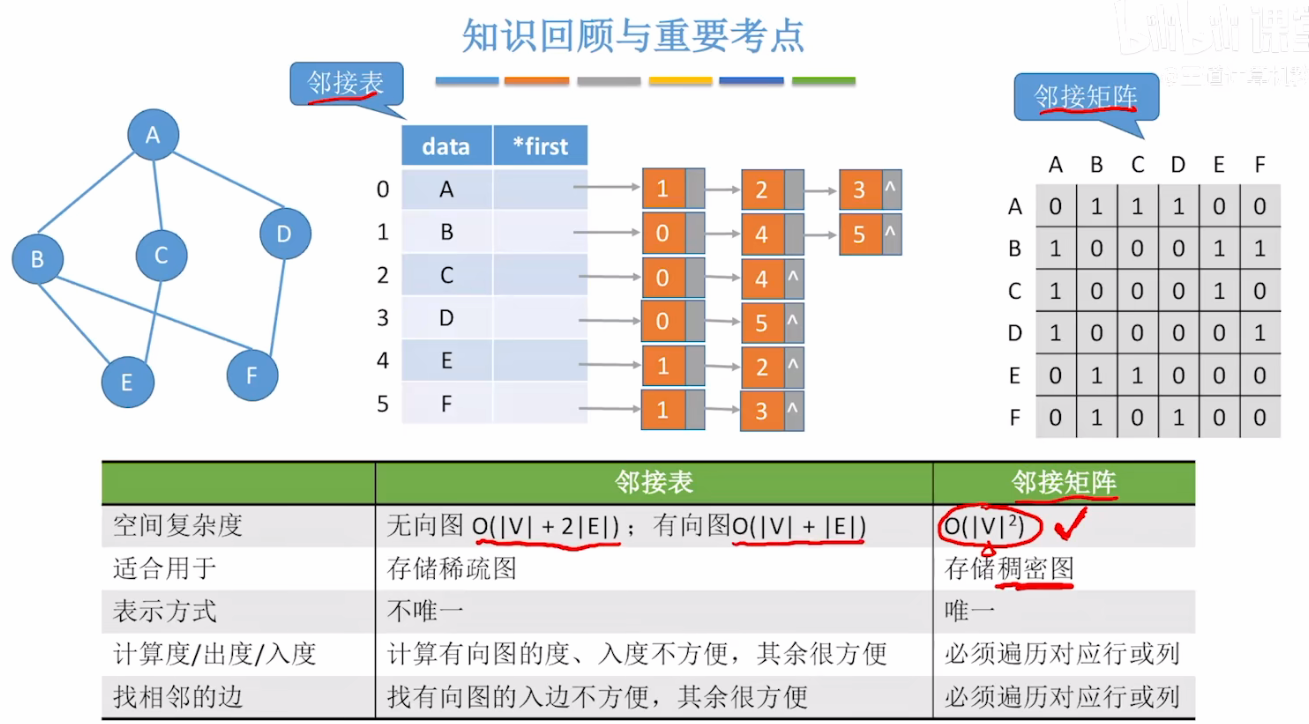
6、与邻接矩阵的核心区别

维度	邻接表法	邻接矩阵法
空间效率	稀疏图占优（O(n+e)）	稠密图占优（O(n²)）
查找边	慢（O(度(v))）	快（O(1)）
遍历邻接点	快（直接遍历链表）	慢（需遍历整行）
实现复杂度	较高（链表操作）	较低（二维数组）
动态扩展性	强（链表增删灵活）	弱（数组大小固定）

选择原则：

• 稀疏图（边数 e ≤ nlogn）→ 优先选邻接表；
• 稠密图（边数接近 n²）→ 优先选邻接矩阵；
• 需频繁查边 → 选邻接矩阵；
• 需频繁遍历邻接点 → 选邻接表.