十.最短路径问题
1.BFS算法
BFS 最短路径
(1)代码
//求顶点u到其他顶点的最短路径
void BFS_MIN_Distance(Graph G,int u){
//d[i]表示从u到i结点的最短路径
for(i=0;i<G.vexnum;++i){
d[i]=∞; //初始化路径长度
path[i]=-1; //最短路径从哪个顶点过来
}
d[u]=0;
visited[u]=TRUE;
EnQueue(Q,u);
while(!isEmpty(Q)){ //BFS算法主过程
DeQueue(Q,u); //队头元素u出队
for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))
if(!visited[w]){ //w为u的尚未访问的邻接顶点
d[w]=d[u]+1; //路径长度加1
path[w]=u; //最短路径应从u到w
visited[w]=TRUE; //设已访问标记
EnQueue(Q,w); //顶点w入队
}//if
}//while
}
(2)图解代码
相比与BFS算法的直接使用,求最短路径问题多了两个数组:d[i],path[i]
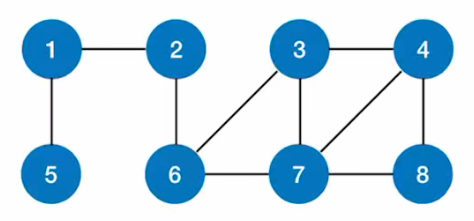例如:我们求从2号顶点到其他顶点的最短路径;
- 首先,初始化两个数组:
d[i]=∞; path[i]=-1;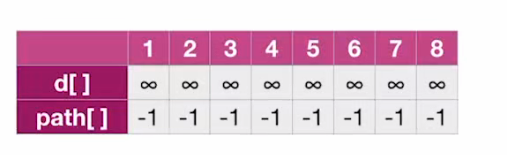
- 然后,将 d[2]=0;(因为2号顶点到2号顶点距离为0);
--d[u]=0; - 然后,像广度优先遍历一样,2号顶点已经被标记过了,将其 visit 值设为 True ;再放入数组中;
--visited[u]=TRUE; EnQueue(Q,u); - 接下来执行 while 循环,如果队列非空,则弹出队头元素:2;
- 然后再进行 for 循环,找到和2相邻的所有顶点;
- 如果该邻接顶点没有被访问过(即 visit 值为False),则路径长度+1;
d[w]=d[u]+1=d[2]+1=0+1=1;所以将d[1]和d[6]的值都改为1; - 还需要记录 path 数组;1和6的最短路径都是由2过来的;所以
path[1]=path[6]=2;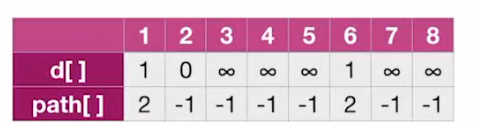
还需将1,6的 visit 值改为 True;
继续进行 while 循环,访问1号顶点;
- 将队头元素:2弹出队列;此时应该访问1的邻接顶点
- 第一个找到的是2号顶点,visit值为True;跳过
- 访问5号顶点:最短路径长度=1号顶点的最短路径长度+1;
d[5]=d[1]+1=2; - path[5]=1;
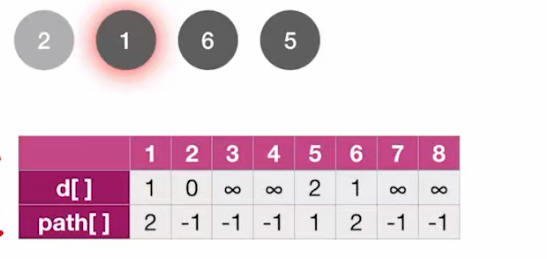
继续处理6号顶点:
- 6号顶点的邻接顶点为3,7;path[3]=path[7]=6;
d[3]=d[7]=d[6]+1=3;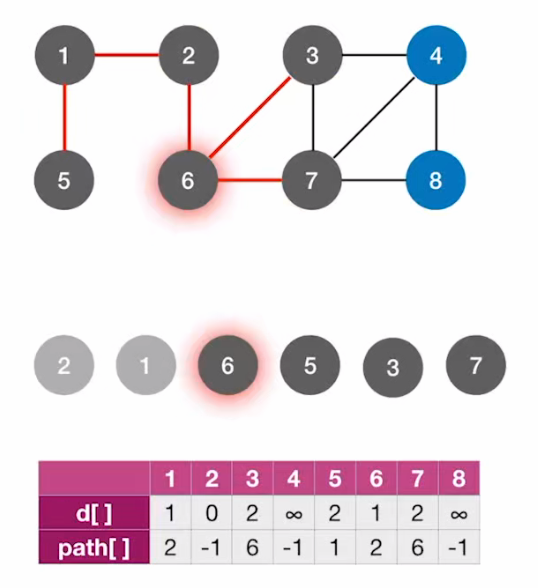
接下来处理5号顶点:
- 5号顶点的所有邻接顶点都被访问过了;跳过;
最终得到: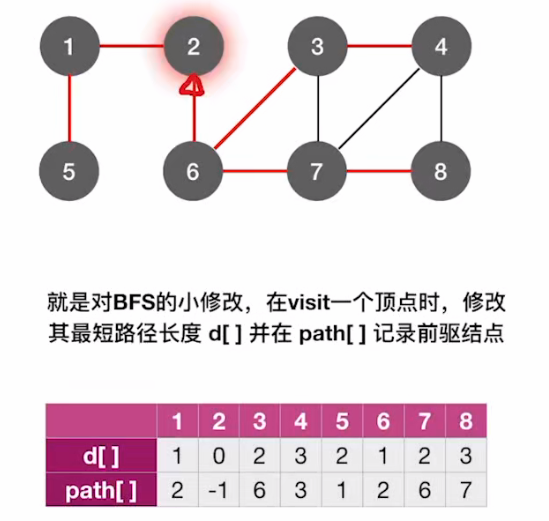
由上图可知:
2->8的最短路径长度=d[8]=3;
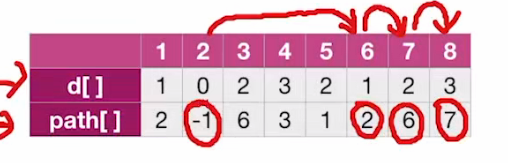
- 8号顶点对应的path值为7;
- 7的path值为6;
- 6的path值为2;
综上:2->6->7->8为最短路径
其实在前面我们构造过广度优先生成树,可以通过观察生成树来得到最短路径.
2.Dijkstra算法
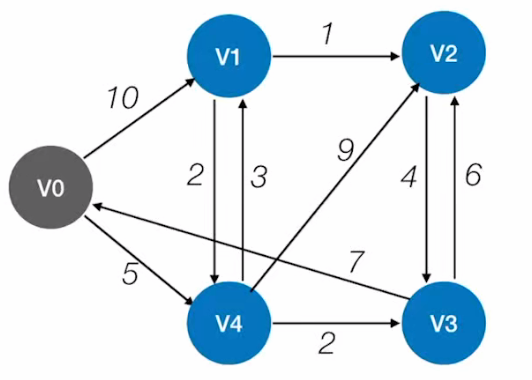
Dijkstra 最短路径
(1)初始化操作
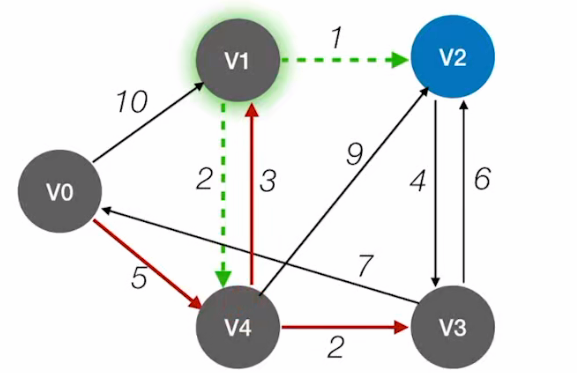
如图所示:
我们从V0开始寻找到各个顶点的最短路径;
首先,初始化三个数组:
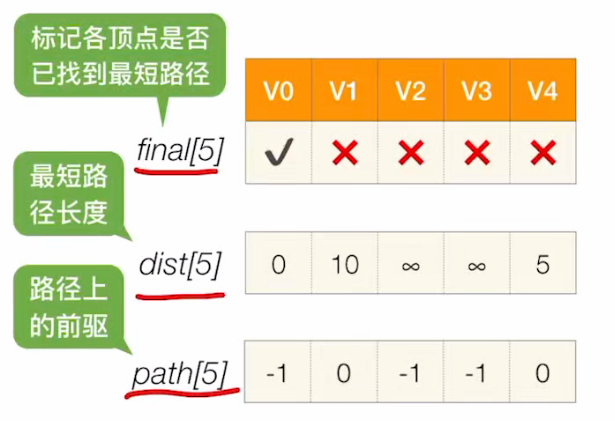
dist数组表示:目前为止可以找到的最短的一条路径长度为多少;
- 首先,V0到自己的最短路径肯定为0;
- 刚开始,我们可以找到一条
V0->V1的边,长度为10;V0->V4,长度为5; - V2,V3并不存在直接从V0过来的边;所以最短路径长度
设为∞;
path数组表示:最短路径上的前驱;
- 所以将V1,V4的path值设为0;
(2)图解代码
第 1 轮：循环遍历所有结点，找到还没确定最短路径、且 dist 最小的顶点 Vi，令 final [i]=ture。
根据初始化的 dist 数组,第1轮遍历的最短路径为5;对应的顶点为V4;将其 final 值设为 True;
检查所有邻接自 Vi 的顶点，若其 final 值为 false，则更新 dist 和 path 信息
查看与V4相邻的顶点:V1,V2,V3;
这些顶点的final值都为False;
先看V1:
如果从V0->V4->V1会不会比V0->V4更短呢?
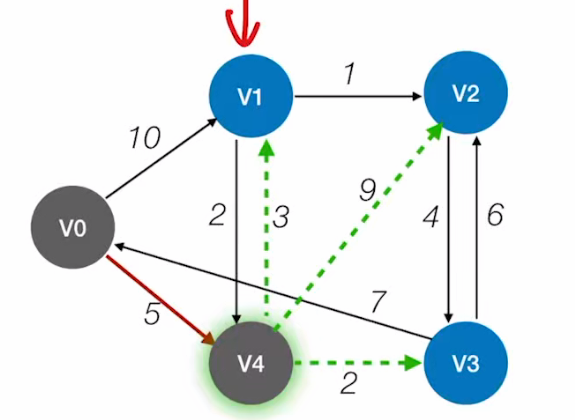由图可知:
V0->V4->V1=5+3=8;
V0->V4=10;
所以,将V1的dist值改为8,path值改为4
此时发现,V0->V4->V2=5+9=14;
所以,将V2的dist值改为14,path值改为4
同理:
所以,将V3的dist值改为7,path值改为4
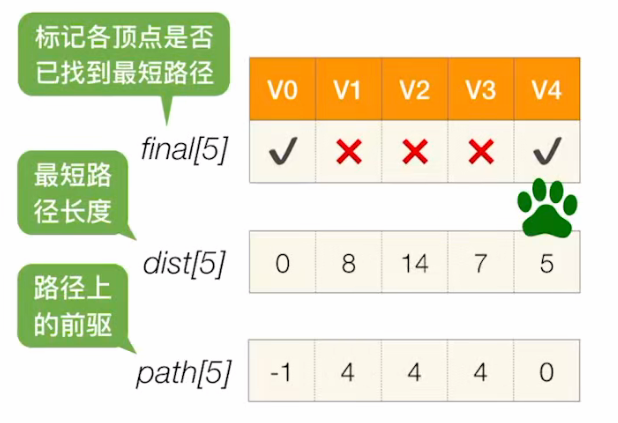
第 2 轮：循环遍历所有结点，找到还没确定最短路径、且 dist 最小的顶点 Vi，令 final [i]=ture。
查看dist数组,其中最小的顶点为V3; 令final[V3]=true;
检查所有邻接自 Vi 的顶点，若其 final 值为 false，则更新 dist 和 path 信息
接下来检查所有可以从V3经过的顶点
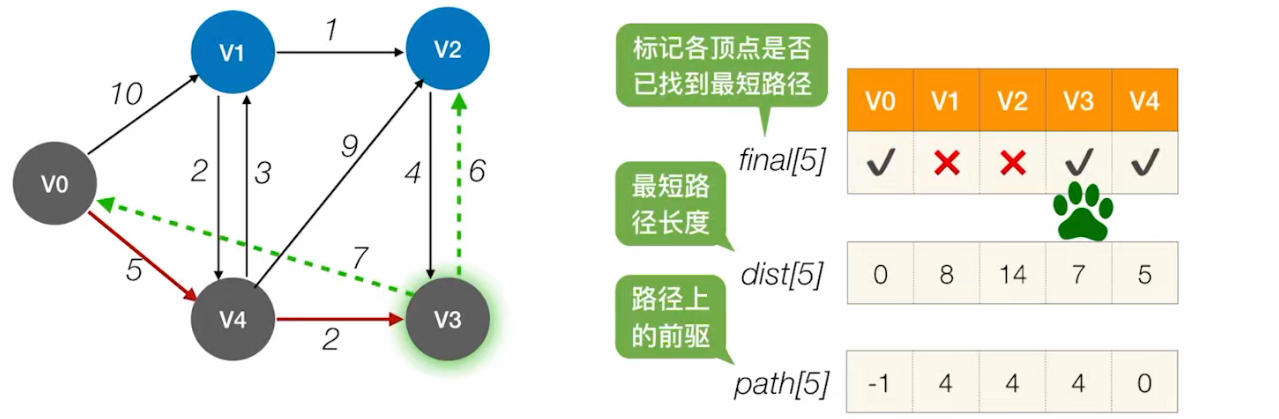
此时发现:
V0->V4->V3->V2=5+2+6=13<14;
所以,将V2的dist值改为13,path值改为3
第 3 轮：循环遍历所有结点，找到还没确定最短路径、且 dist 最小的顶点 Vi，令 final [i]=ture。
此时dist最小值的顶点为V1,令final[V1]=true;
检查V1的邻接顶点,为V2,V4;
其中V4的最短路径已经确定;只需检查V2;
此时发现:
V0->V4->V1->V2=dist[V1]+1=9;
所以,将V2的dist值改为9,path值改为1
第 4 轮：循环遍历所有结点，找到还没确定最短路径、且 dist 最小的顶点 Vi，令 final [i]=ture。
最后只剩下V2顶点,
但是找不到final值为False的顶点了;
算法到此结束.
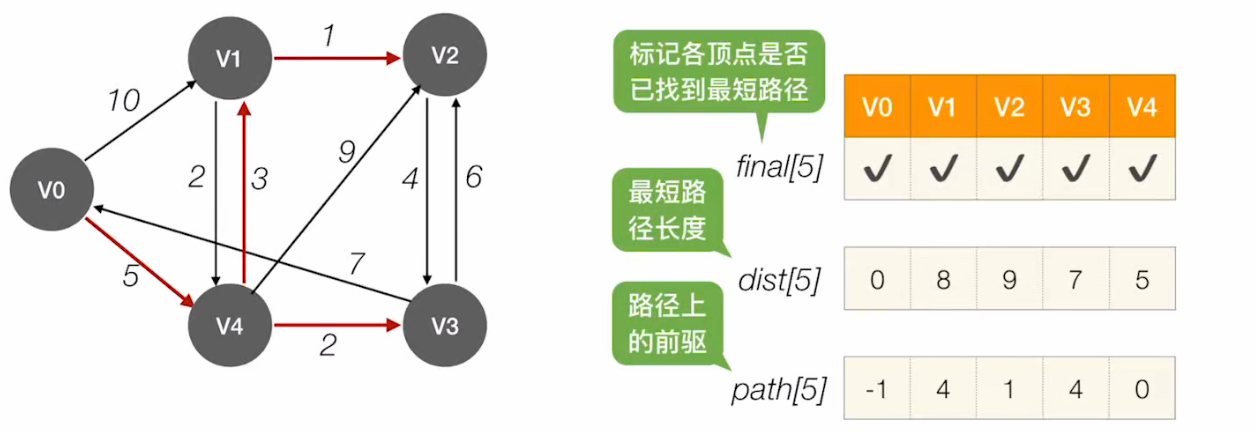
V0 到 V2 的最短 (带权) 路径长度为：dist [2] = 9;
通过 path [] 可知，V0 到 V2 的最短 (带权) 路径：V2 <-- V1 <-- V4 <-- V0
结论：Dijkstra 算法不适用于有负权值的带权图
3.Floyd算法
Floyd 多源最短路径
(1)原理
Floyd 算法：
求出每一对顶点之间的最短路径使用动态规划思想，将问题的求解分为多个阶段对于 n 个顶点的图 G，求任意一对顶点 Vi -> Vj 之间的最短路径可分为如下几个阶段：
#初始：不允许在其他顶点中转，最短路径是？
#0：若允许在 V₀中转，最短路径是？#1：若允许在 V₀、V₁中转，最短路径是？
#2：若允许在 V₀、V₁、V₂中转，最短路径是？
...
#n-1：若允许在 V₀、V₁、V₂……Vₙ₋₁中转，最短路径是？
(2)代码
//……准备工作，根据图的信息初始化矩阵A和path（如上图）
for (int k=0; k<n; k++){ //考虑以Vk作为中转点
for(int i=0; i<n; i++) { //遍历整个矩阵，i为行号，j为列号
for (int j=0; j<n; j++){
if (A[i][j]>A[i][k]+A[k][j]){ //以vk为中转点的路径更短
A[i][j]=A[i][k]+A[k][j]; //更新最短路径长度
path[i][j]=k; //中转点
}
}
}
}
(3)图解代码
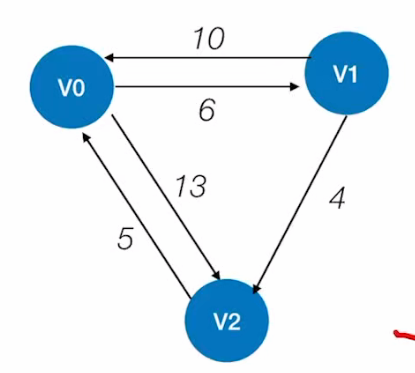
首先,由上图得到 A矩阵 和 path矩阵
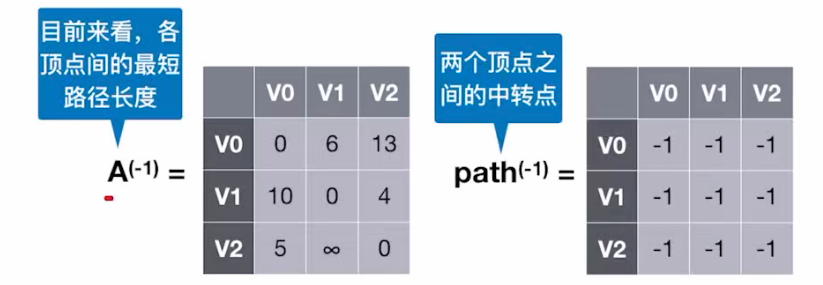A矩阵就是图的邻接矩阵;
初始状态,都不存在中转顶点,初始为-1;
(4)示例
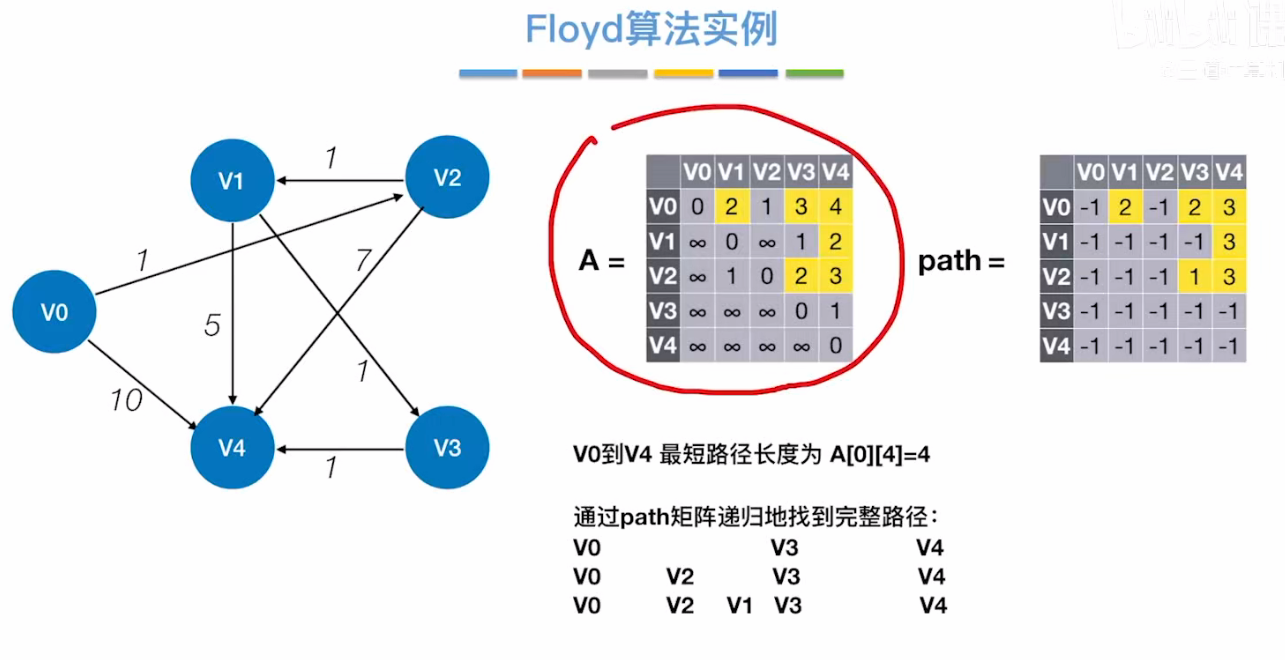
第 1 步:
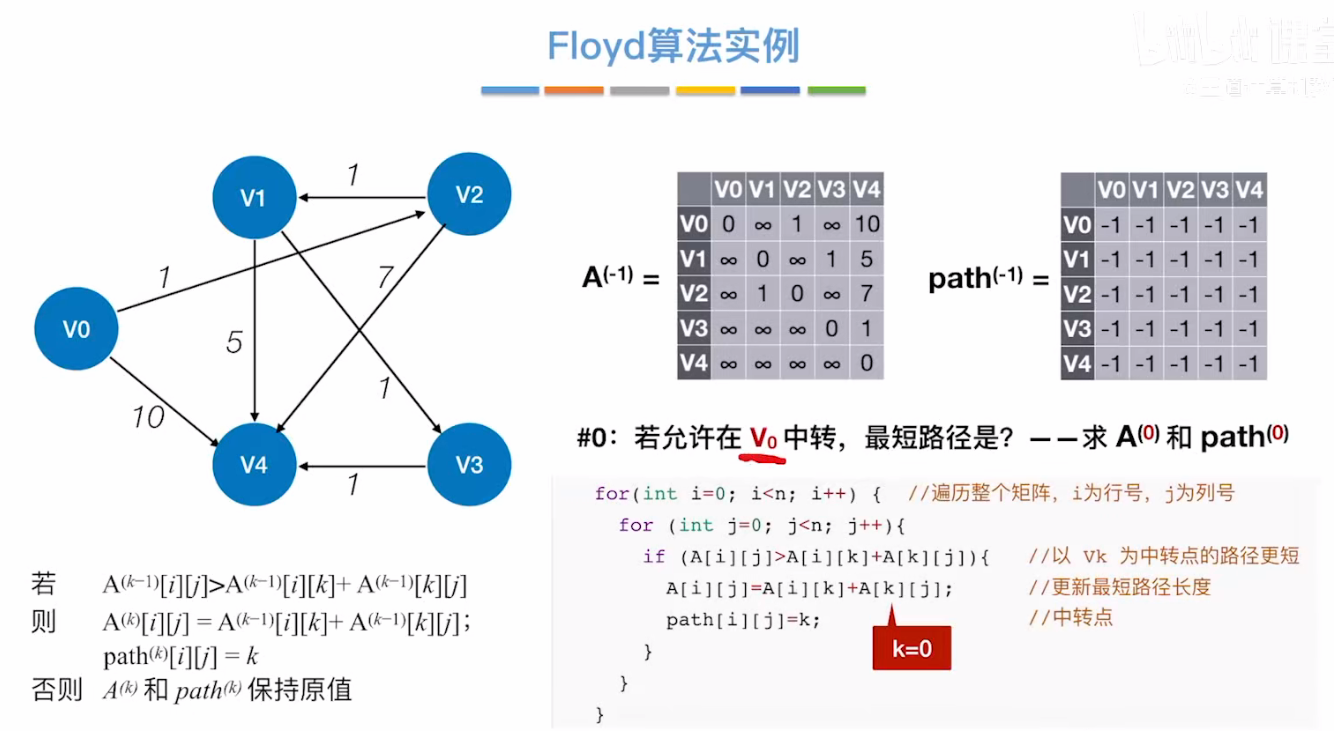
#0：若允许在 V₀中转，最短路径是？—— 求 A⁽⁰⁾和 path⁽⁰⁾
因为V2到V1没有直达的线,所以我们考虑使用V0做中转点;V2->V1->V0
如上图:
将 i=2,j=1,k=0 带入公式中;
得到:
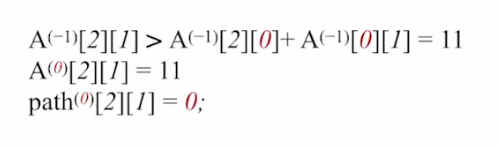经过V0中转点后长度变为11,比原来的∞距离更近
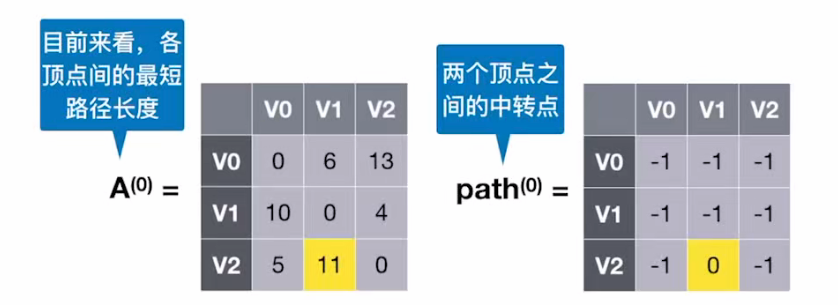
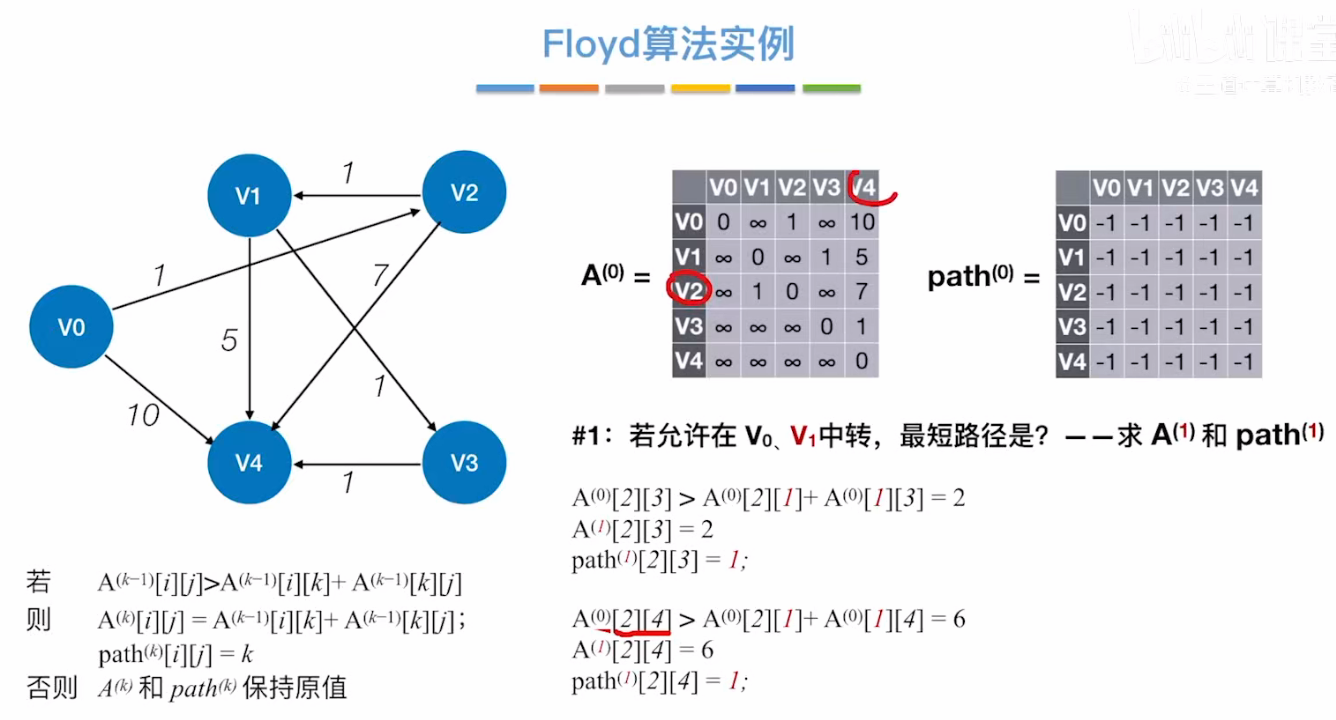
第 2 步:
#1：若允许在 V₀、V₁中转，最短路径是？—— 求 A⁽¹⁾和 path⁽¹⁾
依次遍历各个顶点
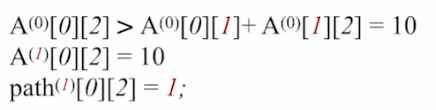
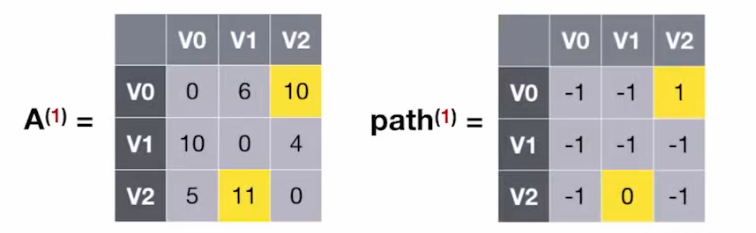
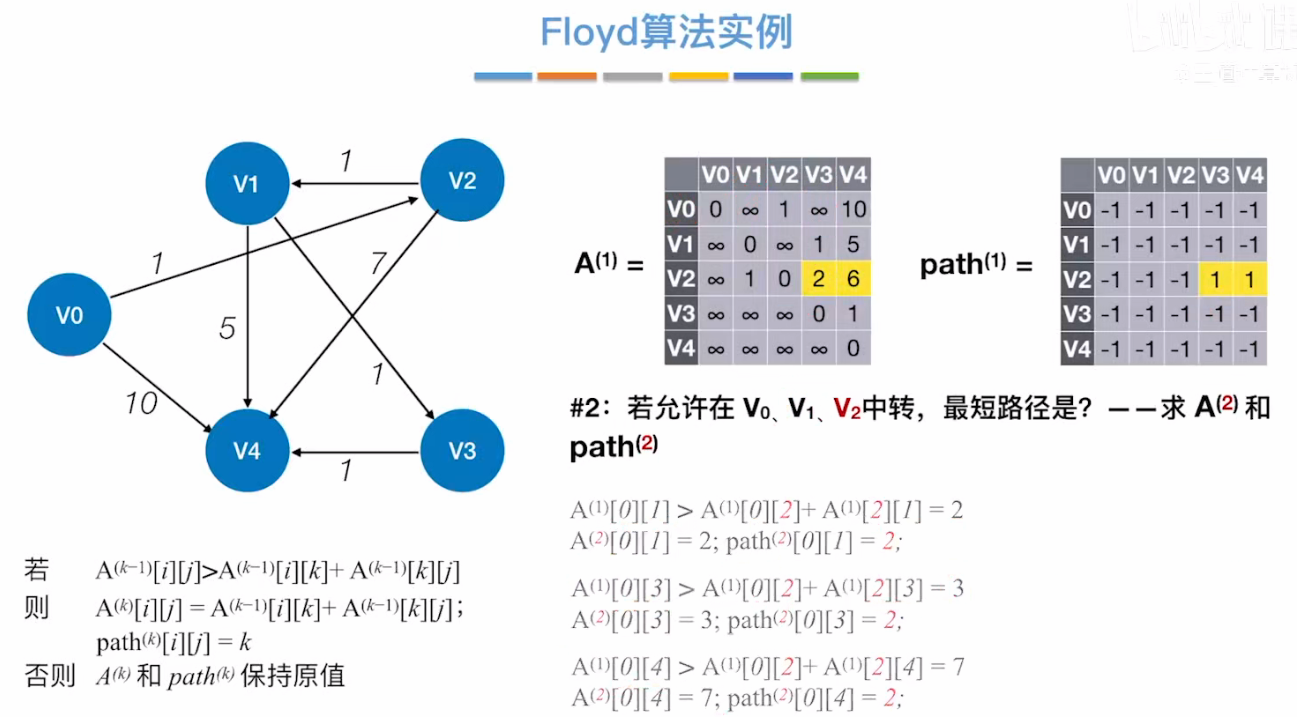
第 3 步:
#2：若允许在 V₀、V₁、V₂中转，最短路径是？—— 求 A⁽²⁾和 path⁽²⁾
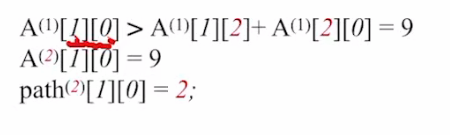
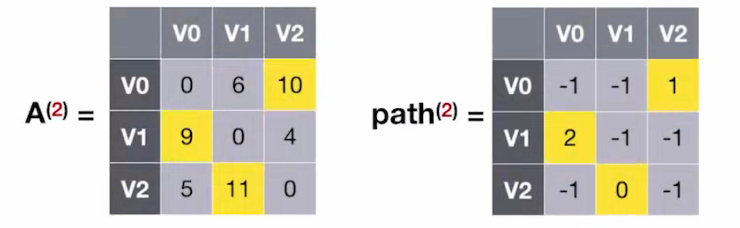
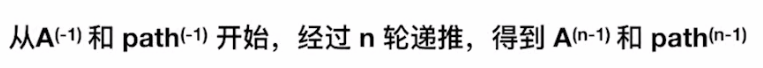
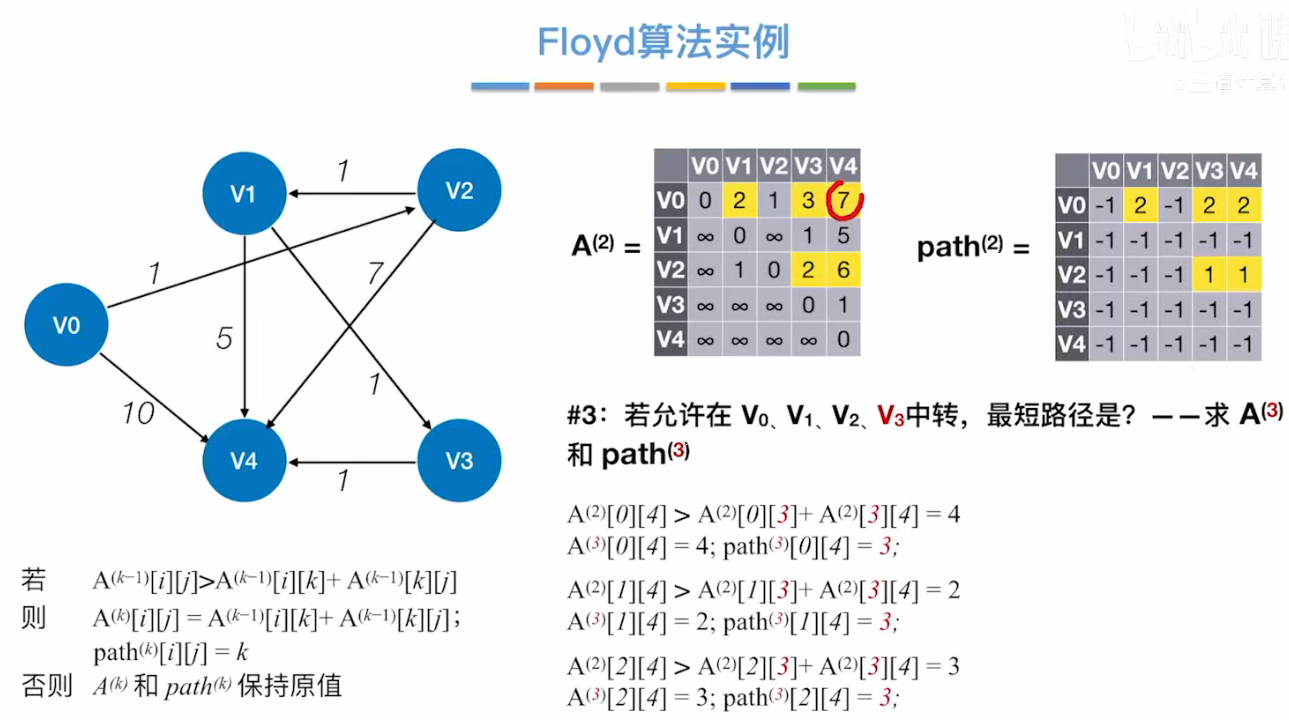
- 根据 A⁽²⁾可知，V1 到 V2 最短路径长度为 4，根据 path⁽²⁾可知，完整路径信息为 V1_V2
- 根据 A⁽²⁾可知，V0 到 V2 最短路径长度为 10，根据 path⁽²⁾可知，完整路径信息为 V0_V1_V2
- 根据 A⁽²⁾可知，V1 到 V0 最短路径长度为 9，根据 path⁽²⁾可知，完整路径信息为 V1_V2_V0
4.对比三种算法
以下是 BFS（无权图最短路径）、Dijkstra（单源带权无负权图）、Floyd（多源带权无负权/负权无环图） 三种最短路径算法的核心对比，用表格+通俗解读的形式呈现，方便理解和记忆：
| 对比维度 | BFS（广度优先搜索） | Dijkstra（迪杰斯特拉） | Floyd（弗洛伊德） |
|---|---|---|---|
| 适用场景 | 无权图 / 所有边权值相同的带权图 | 单源最短路径（一个起点→所有其他点）<br / />带权图（边权≥0，无负权） | 多源最短路径（任意两点间）<br / />带权图（可含负权边，但不能有负权环） |
| 核心思想 | 层层扩散，先访问的点就是最短路径（步数最少） | 贪心策略：每次选“当前离起点最近的未确定点”，更新其邻点距离 | 动态规划：逐步解锁中转点，尝试“i→k→j”替代“i→j”，更新最短距离 |
| 时间复杂度 | 邻接表：O(n+m)（n=顶点数，m=边数） 邻接矩阵：O(n²) | 邻接矩阵：O(n²) 邻接表+优先队列：O(m log n) | 固定O(n³)（三层循环：n个中转点×n行×n列） |
| 空间复杂度 | O(n)（队列+访问标记+距离/路径数组） | O(n)（距离数组+标记数组+路径数组） | O(n²)（距离矩阵A + 路径矩阵path） |
| 能否处理负权 | 仅支持无权/等权，无“负权”概念 | ❌ 不支持（负权会破坏贪心策略，导致结果错误） | ✅ 支持负权边（但负权环会导致路径长度无限缩短，无法求解） |
| 起点数量 | 单源（一次只能求一个起点的最短路径） | 单源 | 多源（一次求完所有点对的最短路径） |
| 实现难度 | 简单（基础遍历逻辑） | 中等（贪心+优先队列/数组找最小值） | 简单（三层循环，代码量极少） |
| 适用图类型 | 稠密/稀疏图均可（稀疏图更优） | 稀疏图（邻接表+优先队列）更优；稠密图（邻接矩阵）也可 | 稠密图更优（n小的时候效率可接受）；n大时O(n³)效率极低 |
补充关键解读（避坑+选型建议）：
BFS：
- 本质是“步数最短”，比如迷宫问题、社交网络好友推荐（最少好友链），边权必须相同才可用；
- 无法处理带权图（比如边权有1、2、3），因为“先访问”不一定是“距离最短”。
Dijkstra：
- 单源场景的首选（比如导航中“从我的位置到所有地点”），效率比Floyd高（尤其是稀疏图）；
- 为什么不支持负权？比如：起点A→B=5，A→C=3，C→B=-1，贪心选C后会认为B的最短距离是2，但Dijkstra会先锁定B的距离5，错过更优解。
Floyd：
- 优势是“代码极简、多源求解”，适合顶点数少的场景（比如n≤100）；
- 若n≥200，O(n³)会超时，此时建议对每个点跑一次Dijkstra（总复杂度O(n×m log n)）更高效；
- 处理负权边时，需先检查图中是否有负权环（有则无解）。
选型口诀：
- 无权/等权图 → BFS；
- 单源、无负权、带权图 → Dijkstra；
- 多源、顶点少、可含负权（无环）→ Floyd；
- 有负权环 → 以上都不行，需用Bellman-Ford/SPFA。