九.最小生成树
1.Prime算法
Prim 算法(普里姆):从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
Prim 最小生成树
-w:
MST Weight: 0
准备就绪
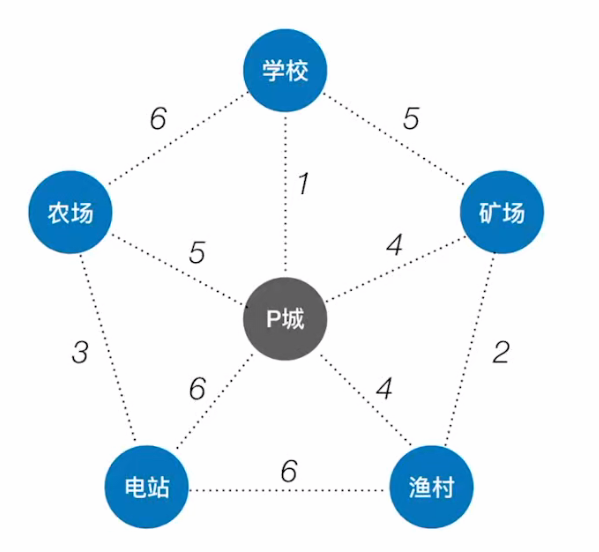 如上图所示:
如上图所示:
- 选取P城当作顶点开始构建生成树;
- 观察与P城相连的代价最小的点,
为学校;将学校纳入生成树中: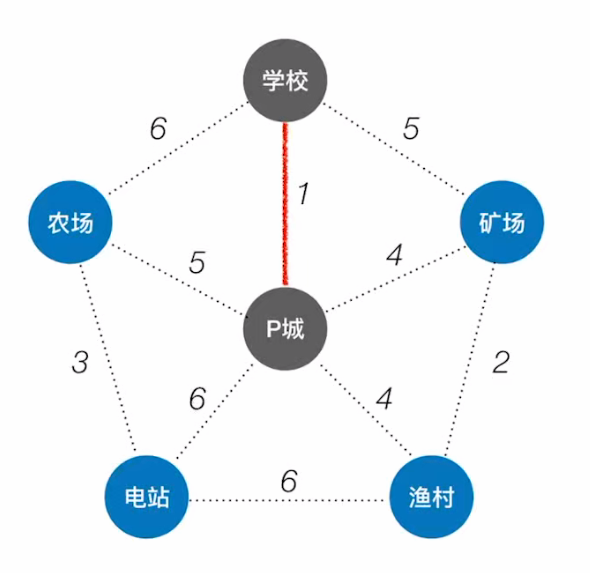
- 观察此时与P城相连的代价最小的顶点为:
矿场和渔村; - 将矿场纳入生成树中;
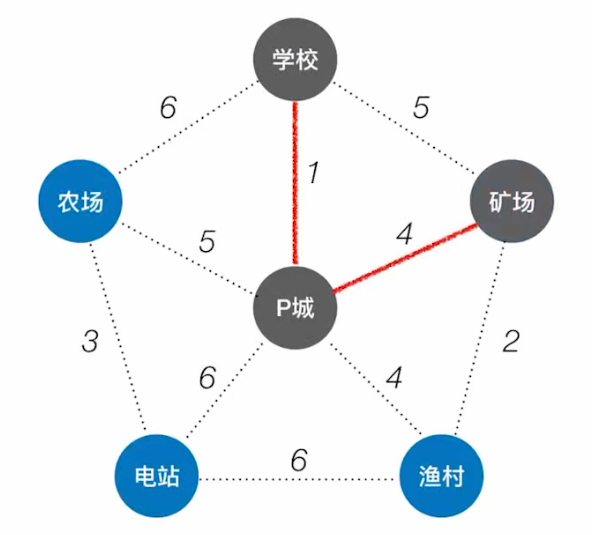
- 此时,学校,P城,矿场构成了一棵生成树;
- 找与这棵树相连的代价最小的顶点:
渔村; - 将渔村纳入生成树;且
与矿场相连;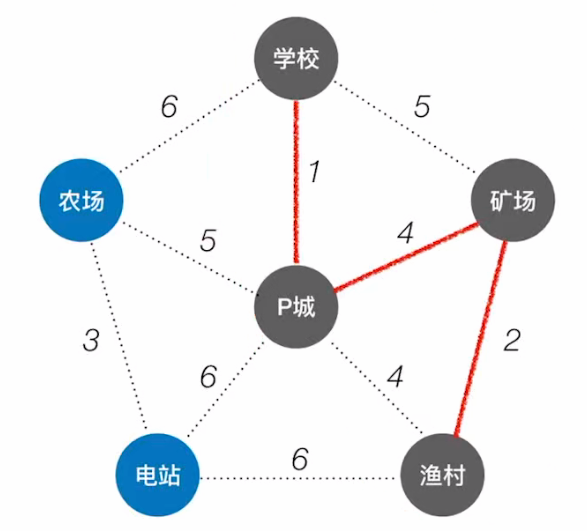
- 此时,P城,矿场,渔村,学校构成了一棵生成树;
- 观察,与此树相连且代价最小的为:农场;
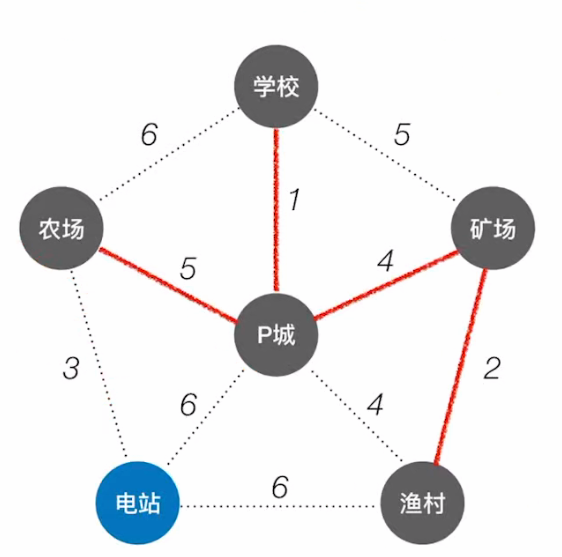
- 最后,电站与农村相连代价最小;
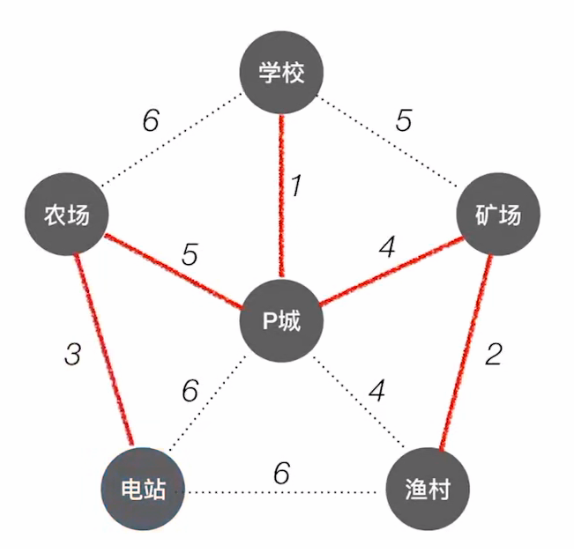
2.Kruskal算法
Kruskal 算法(克鲁斯卡尔):每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选),直到所有结点都连通
Kruskal 最小生成树
-w:
MST Weight: 0
准备就绪
 如上图所示:
如上图所示:
- 观察,权值最小的边为:
P城 -> 学校; - 将其连通;
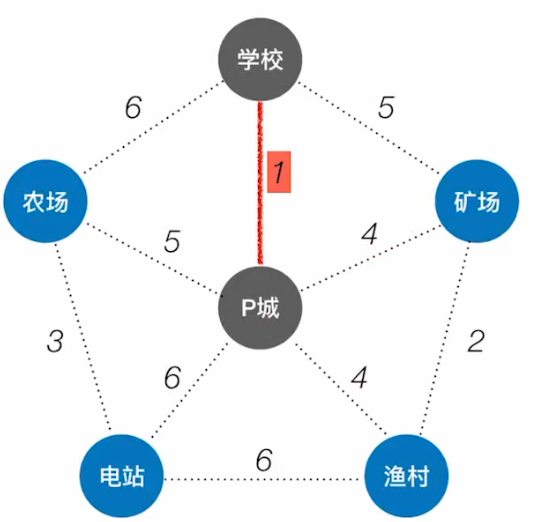 继续连接:
继续连接: - 往下两步,权值最小的为:2,3;
- 连接:
农场 -> 电站,矿场 -> 渔村;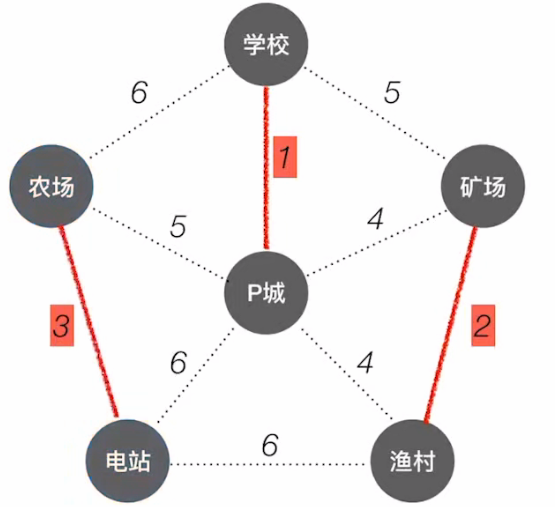
继续:
下一个权值小的为4;
存在:
P城 -> 矿场,P城 -> 渔村;二选一;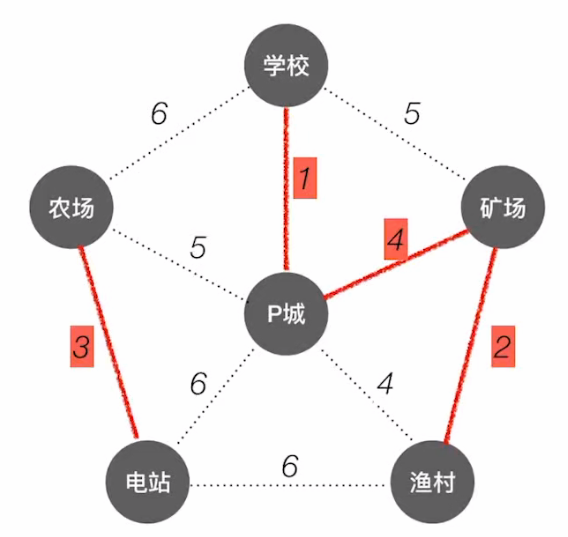 观察上图:
观察上图:此时继续查找;发现权值最小:4,P城 -> 渔村,其两端已经被连通了;
所以
不选;此时发现,剩下的权值最小且还没有连通的为:
农场 -> P城;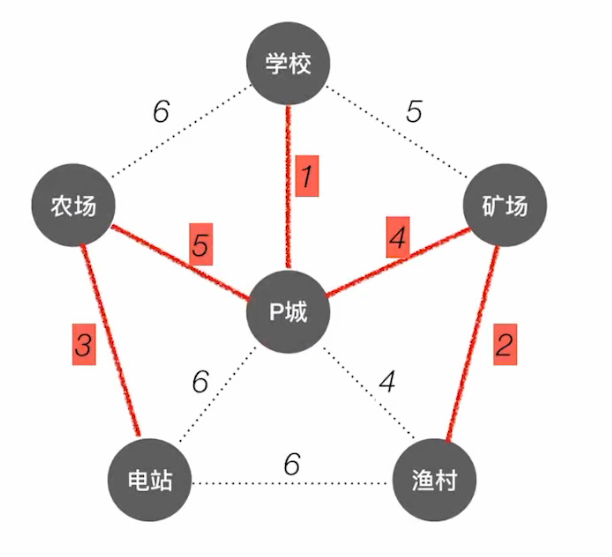
Ending.
3.时间复杂度
Prime算法:
时间复杂度:O (|V|²)适合用于边稠密图
Kruskal算法:
时间复杂度:O (|E|log₂|E|)适合用于边稀疏图