跳到主要内容

十一、树的存储结构

树与森林的存储结构演示​

下方演示了树和森林在三种不同存储结构下的内存形态。点击上方按钮可切换不同场景。

1. 双亲表示法 (树)

逻辑结构 (树/森林)

RABCDE

物理存储 (双亲表示法 - 数组)

下标
数据
双亲
0
R
-1
1
A
0
2
B
0
3
C
1
4
D
1
5
E
2

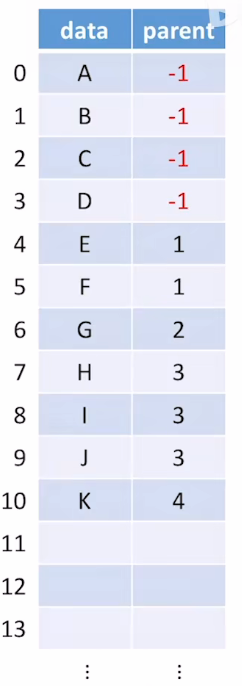
1.树的存储1:双亲表示法(顺序存储)​

Img

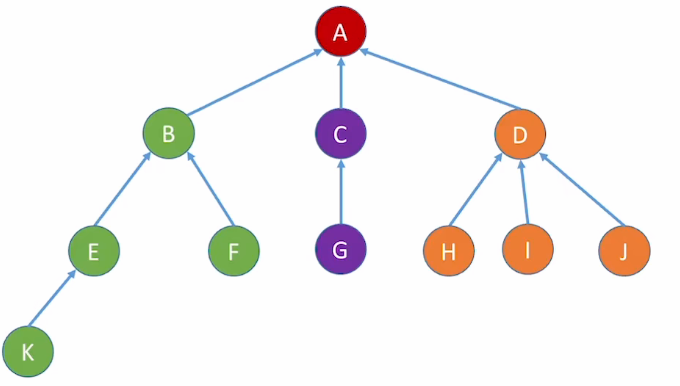
  • 思路:用数组顺序存储各个结点.每个结点中保持数据元素,指向双亲结点(父结点)的"指针" 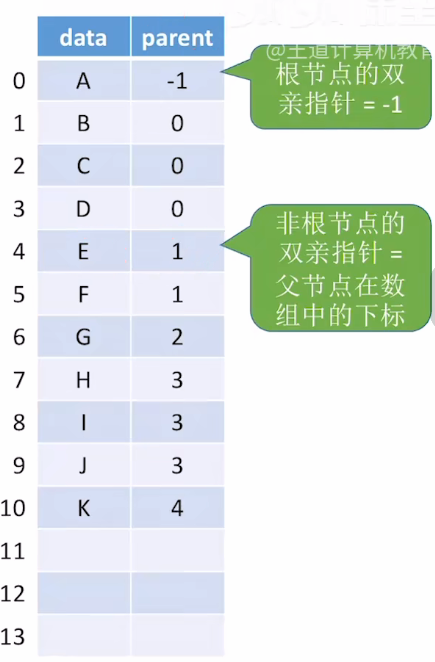Img{: height="300px"}
#define MAX_TREE_SIZE 100

typedef struct {       //树的结点定义
    ElemType data;     //数据元素
    int parent;        //双亲位置域
}PTNode;

typedef struct {       //树的类型定义
    PTNode nodes[MAX_TREE_SIZE];   //双亲表示
    int n;     //结点数
}PTree;

双亲表示法

  • 优点：找双亲（父节点）很方便
  • 缺点：找孩子不方便，只能从头到尾遍历整个数组 适用于“找父亲”多，“找孩子”少的应用场景。如：并查集

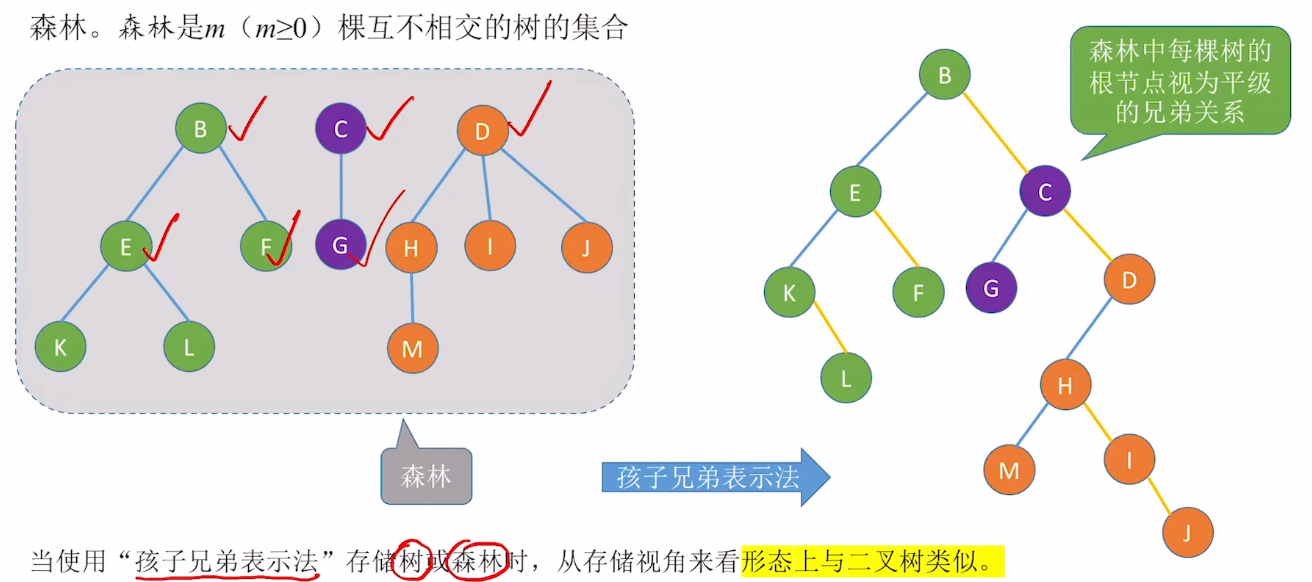
2.拓展:双亲表示法存储"森林"​

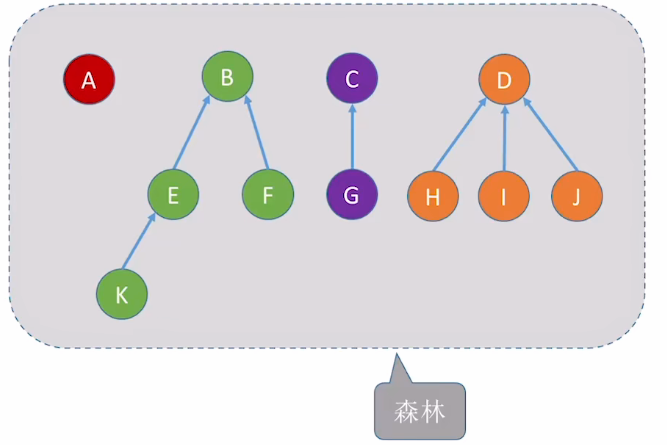
  • 森林.森林是 m (m>=0) 棵互不相交的树的集合 ImgImg{: height="300px"}

3.树的存储2:孩子表示法(顺序+链式)​

  • 首先一个数组元素中包含data和一个链表的指针;
typedef struct {
    ElemType data;
    struct CTNode* firstChild;   //第一个孩子
}CTBox;
  • 而链表结点当中只需要保持孩子的编号以及指向下一个链表的指针就可以;
struct CTNode {
    int child;
    struct CTNode* next;
};
  • 然后用刚才定义的结构体CTBox去声明一个数组,在数组中存储各个结点的信息,还需要知道一共有多少结点,以及根结点的位置下标;
typedef struct {
    CTBox nodes[MAX_TREE_SIZE];
    int n, r;
};

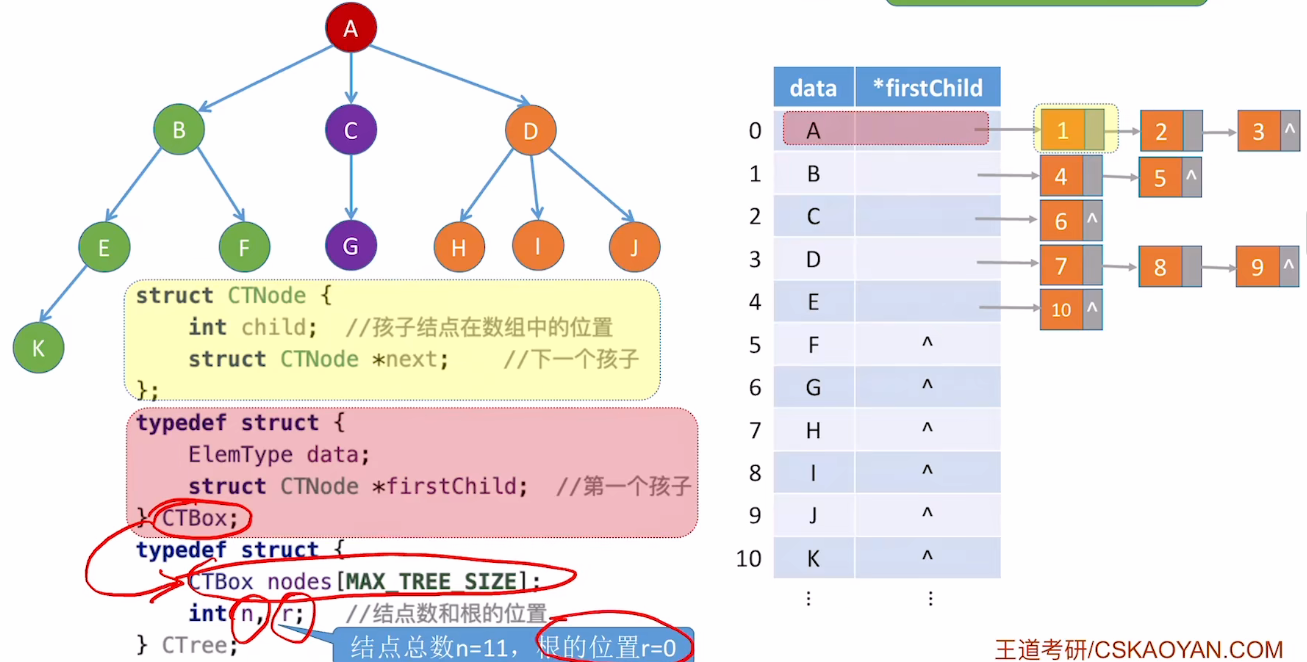Img 孩子表示法

  • 优点：找孩子很方便
  • 缺点：找双亲（父节点）不方便，只能遍历每个链表 适用于“找孩子”多，“找父亲”少的应用场景。如：服务流程树

4.拓展:孩子表示法存储"森林"​

Img

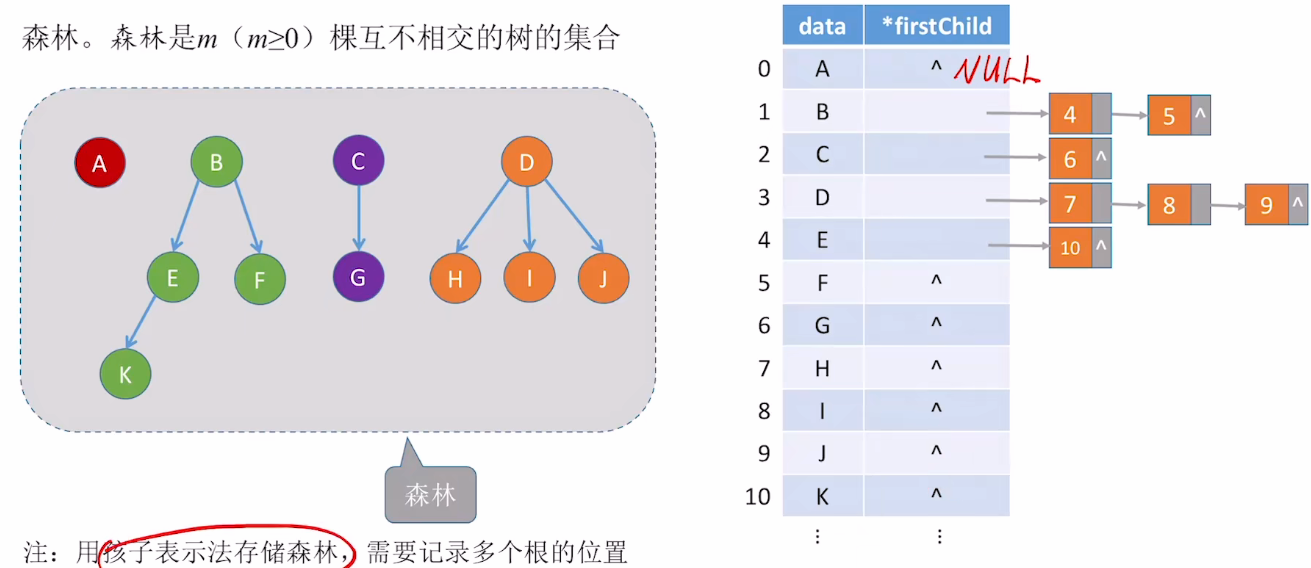
5.树的存储3:孩子兄弟表示法​

  • 树的孩子兄弟表示法，与二叉树类似，采用二叉链表实现每个结点内保存数据元素和两个指针，但两个指针的含义与二叉树结点不同
//树的存储--孩子兄弟表示法
typedef struct CSNode {
    ElemType data;     //数据域
    struct CSNode* firstchild, * nextsibling;     //第一个孩子和右兄弟指针
}CSNode,*CSTree;
//二叉树的结点(链式存储)
typedef struct BiTNode {
    ElemType data;
    struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;

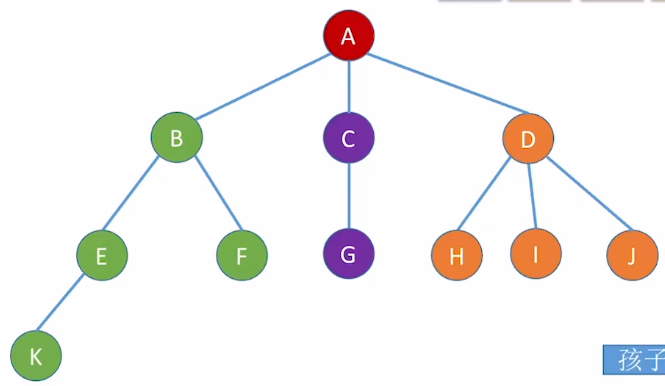Img 如上图:

  • A结点的左孩子是B结点,而A没有右兄弟; 所以A结点左指针指向B,右指针指向NULL; 得到下图: Img

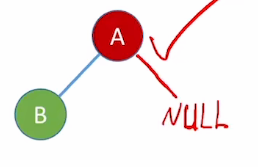
  • 又因为C结点为B结点的右兄弟, 所以,C结点应该连到B结点的右指针; 得到下图: Img

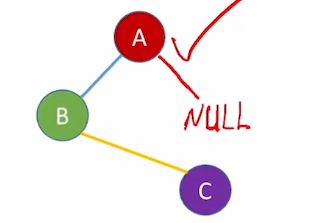
  • 按照这种方式, 最终得到: Img

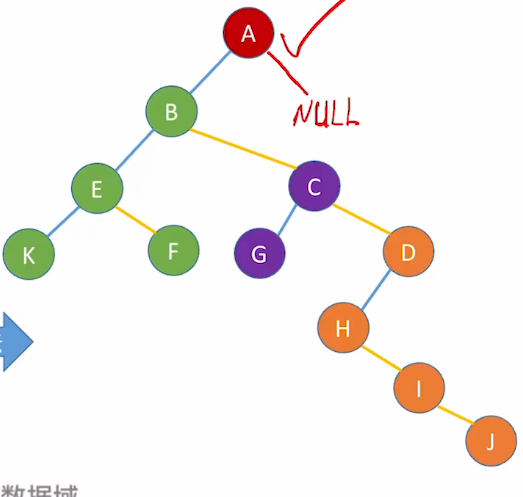
6.拓展:孩子兄弟表示法存储"森林"​

Img

💬 留下你的问题或见解