十、在线索二叉树中找前驱后继

1.中序线索二叉树找中序后继

核心逻辑：如果右指针是线索，直接返回；如果是孩子，则找右子树的最左节点。

规律：若有右子树，则后继是右子树的“最左下”节点。

⏳ 正在初始化演示数据...

(1)图解示例

在中序线索二叉树中找到指定结点*p的中序后继next ① 若 p->rtag == 1，
则 next = p->rchild；

② 若 p->rtag == 0，
则说明p必有右孩子 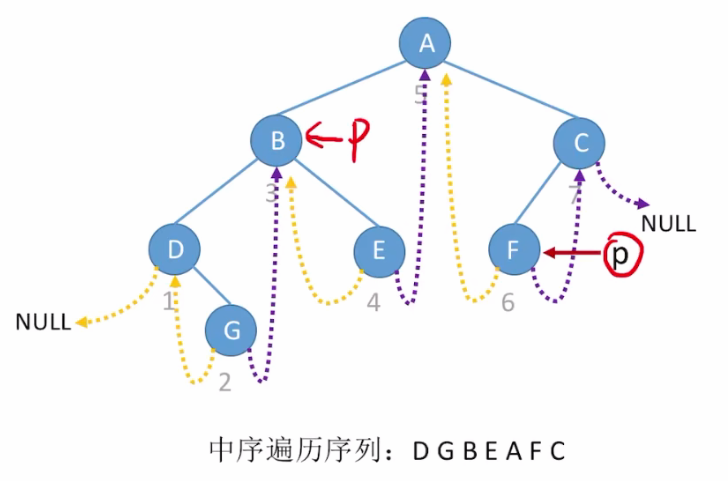如上图所示:

• 当p指针指向F时,rtag=1,说明右结点被线索化,右孩子指针指向中序后继;
• 如果右结点没有被线索化,如p指针指向B结点,rtag=0;说明p必有右孩子,所以要看中序遍历,一个结点被访问的后一个结点是谁;
• 因为中序遍历顺序为:左根右,所以接下来右子树中第一个被遍历的结点就是p的后继结点 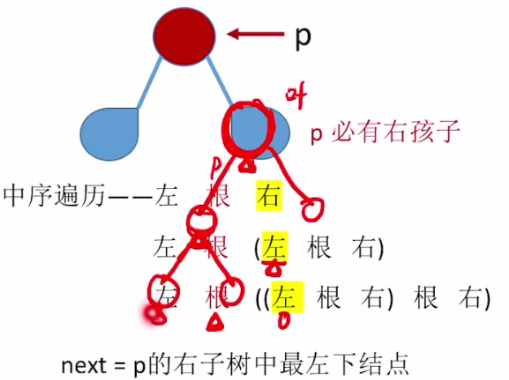如上图所示: 根据中序遍历顺序为:左根右,所以右子树最左下的结点即为p的后继结点

(2)代码

//找到以P为根的子树中,第一个被中序遍历的结点
ThreadNode* Firstnode(ThreadNode* p) {
    //循环找到最左下的结点(不一定是叶结点)
    while (p->ltag == 0)
        p = p->lchild;
    return p;
}

//在中序线索二叉树中找到结点p的后继结点
ThreadNode* Nextnode(ThreadNode* p) {
    //右子树中最左下结点
    if (p->rtag == 0)
        return Firstnode(p->rchild);
    else
        return p->rchild;     //rtag==1直接返回后继线索
}

//对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)
void Inorder(ThreadNode* T) {
    for (ThreadNOde* p = Firstnode(T);p != NULL;p = Nextnode(p))
        visit(p);
}

2.中序线索二叉树找中序前驱

规律：若有左子树，则前驱是左子树的“最右下”节点。

⏳ 正在初始化演示数据...

(1)图解示例

在中序线索二叉树中找到指定结点*p的中序前驱pre ① 若 p->ltag == 1，
则 next = p->lchild；

② 若 p->ltag == 0，
则说明p必有左孩子

方法类似

• 如果左孩子已经被线索化,那么左指针指向的结点就是前驱;
• 如果没有被线索化,那就说明一定有左孩子 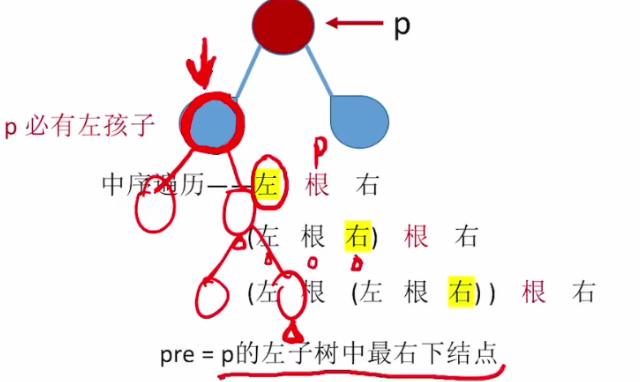根据中序遍历顺序为:左根右,所以左子树最右下的结点即为p的前驱结点

(2)代码

//找到以P为根的子树中,最后一个被中序遍历的结点
ThreadNode* Lastnode(ThreadNode* p) {
    //循环找到最右下结点(不一定是叶结点)
    while (p->rtag == 0)
        p = p->rchild;
    return p;
}

//在中序线索二叉树中找到结点p的前驱结点
ThreadNode* Prenode(ThreadNode* p) {
    //左子树最右下结点
    if (p->ltag == 0)
        return Lastnode(p->lchild);
    else
        return p->lchild;      //ltag==1直接返回前驱线索
}

//对中序线索二叉树进行逆向中序遍历
void RevInorder(ThreadNode* T) {
    for (ThreadNode* p = Lastnode(T);p != NULL;p = Prenode(p))
        visit(p);
}

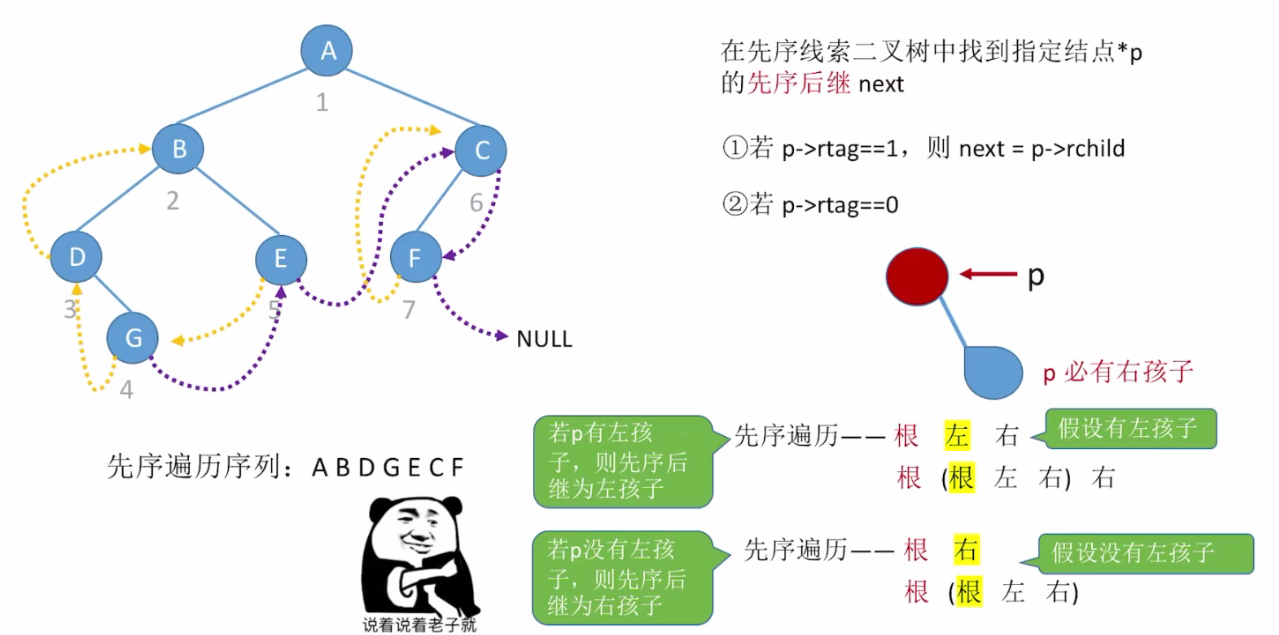
3.先序线索二叉树找先序后继

规律：简单。有左孩子就是左孩子，没左孩子就是右孩子（线索）。

⏳ 正在初始化演示数据...

4. 先序线索二叉树找先序前驱 (Pre) - 🔴 难点

注意：在先序线索树中，找不到前驱是比较麻烦的。因为 ltag=0 时左指针指向的是后继（子节点），无法回溯。必须依赖 父节点指针 (parent)。

⏳ 正在初始化演示数据...

---

5. 后续线索二叉树找后序后继 (Next) - 🔴 难点

注意：同理，后序线索树找后继也很麻烦，必须依赖 父节点指针。

⏳ 正在初始化演示数据...

6. 后续线索二叉树找后序前驱 (Pre)

规律：简单。有右孩子就是右孩子，没右孩子就是左孩子。

⏳ 正在初始化演示数据...