八、线索二叉树讲解

线索二叉树讲解（含存储结构整合）

1、什么是线索二叉树

在普通二叉树中，存在大量空指针（叶子节点的左右指针为空，非叶子节点的部分子节点指针也为空）。线索二叉树是一种对二叉树的优化结构，它利用这些空指针来存储节点的“前驱”和“后继”信息（即该节点在某种遍历序列中的前一个和后一个节点），这些被利用的空指针称为“线索”。

2、存储结构设计（核心：标记位 + 指针域）

为了区分指针是“指向子节点”还是“指向线索”，线索二叉树的节点需增加两个标记位，结构如下（以C语言为例）：

typedef struct ThreadedBinaryTreeNode {
    int data;                // 数据域
    int ltag, rtag;          // 左、右标记位（0=指向子节点，1=指向线索）
    struct ThreadedBinaryTreeNode *lchild; // 左指针（子节点/前驱线索）
    struct ThreadedBinaryTreeNode *rchild; // 右指针（子节点/后继线索）
} ThreadNode, *ThreadTree;

标记位约定： | 标记位 | 值 | 指针含义 | |--------|----|------------------------| | ltag | 0 | 左指针指向左子节点 | | ltag | 1 | 左指针指向前驱线索 | | rtag | 0 | 右指针指向右子节点 | | rtag | 1 | 右指针指向后继线索 |

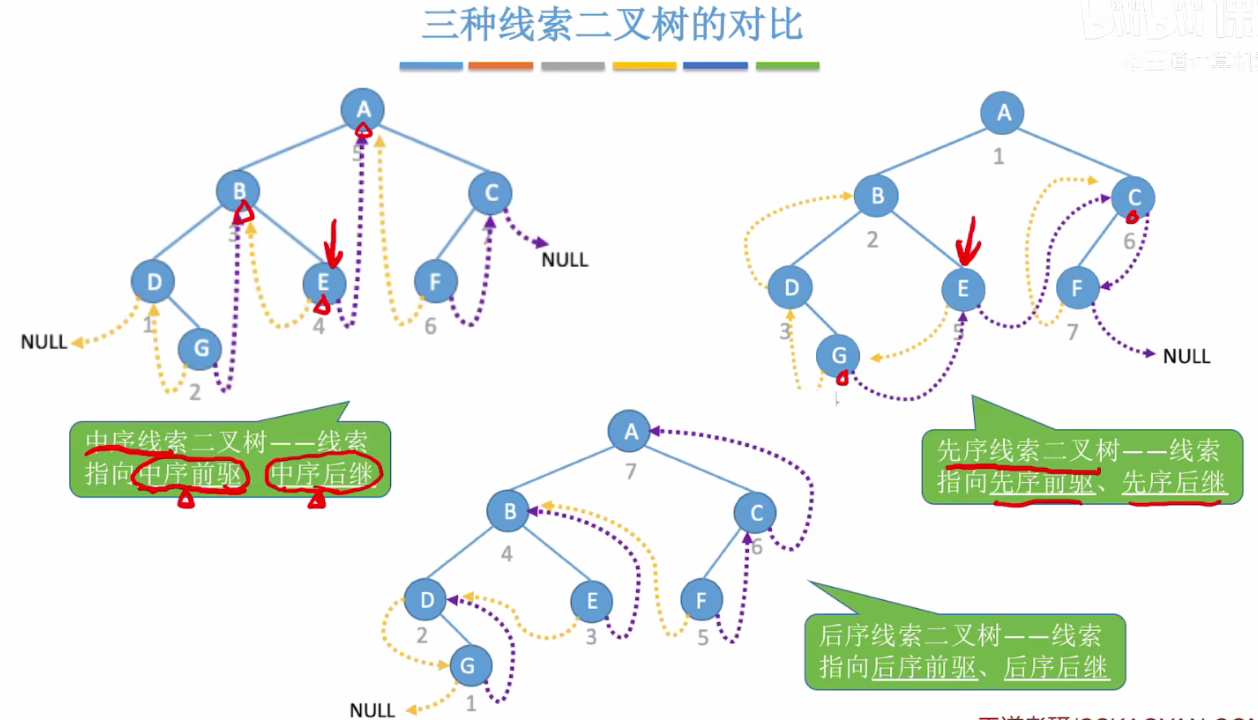
3、线索的分类与遍历关联

线索的指向逻辑与遍历序列类型（中序、前序、后序）强相关，不同遍历下“前驱/后继”的定义不同：

遍历类型	左线索（ltag=1时）	右线索（rtag=1时）
中序线索	中序遍历的前驱节点	中序遍历的后继节点
前序线索	前序遍历的前驱节点	前序遍历的后继节点
后序线索	后序遍历的前驱节点	后序遍历的后继节点

4、线索二叉树的构建（以中序线索化为例）

核心是在遍历过程中记录当前节点的前驱，并通过标记位和指针域建立线索关联。

递归实现步骤：

1. 线索化左子树；
2. 处理当前节点：
   • 若左子树为空，设置 ltag=1，左指针指向前驱；
   • 若前驱的右子树为空，设置前驱的 rtag=1，右指针指向当前节点；
   • 更新前驱为当前节点；
3. 线索化右子树。

5、遍历与存储结构的协同（以中序遍历为例）

利用线索可实现无递归、无栈的高效遍历（空间复杂度$O(1)$）：

1. 找中序第一个节点：从根节点出发，沿左指针循环，直到ltag=1的节点；
2. 找后继节点：
   • 若当前节点rtag=1，直接沿右线索跳转；
   • 若rtag=0，则找右子树的最左节点（中序遍历的后继逻辑）；
3. 循环直到节点为空。

6、工程扩展：带头节点的线索二叉树

为简化边界处理（第一个节点无前驱、最后一个节点无后继），可增加头节点：

• 头节点ltag=0，lchild指向根节点；
• 头节点rtag=1，rchild指向中序最后一个节点；
• 原树第一个节点的lchild指向头节点（前驱线索）；
• 原树最后一个节点的rchild指向头节点（后继线索）。

7、应用与存储特性

• 空间效率：仅增加2个整型标记位，复用$n+1$个空指针，几乎无额外开销；
• 时间效率：遍历、前驱/后继查找的时间复杂度均为$O(n)$，且无递归/栈开销；
• 适用场景：静态二叉树（结构稳定）、需频繁遍历/查找前驱后继的场景（如二叉搜索树）。

示例（中序线索二叉树存储） 二叉树 A(D(B,E),C) 中序遍历为 B→D→E→A→C，其节点存储结构如下：

节点	ltag	lchild	data	rchild	rtag
B	1	NULL	B	D	1
D	0	B	D	E	0
E	1	D	E	A	1
A	0	D	A	C	0
C	1	A	C	NULL	1

线索二叉树通过“标记位+指针域”的存储设计，在不增加过多内存的前提下，实现了空指针的高效复用，是二叉树在遍历优化场景下的经典解决方案。