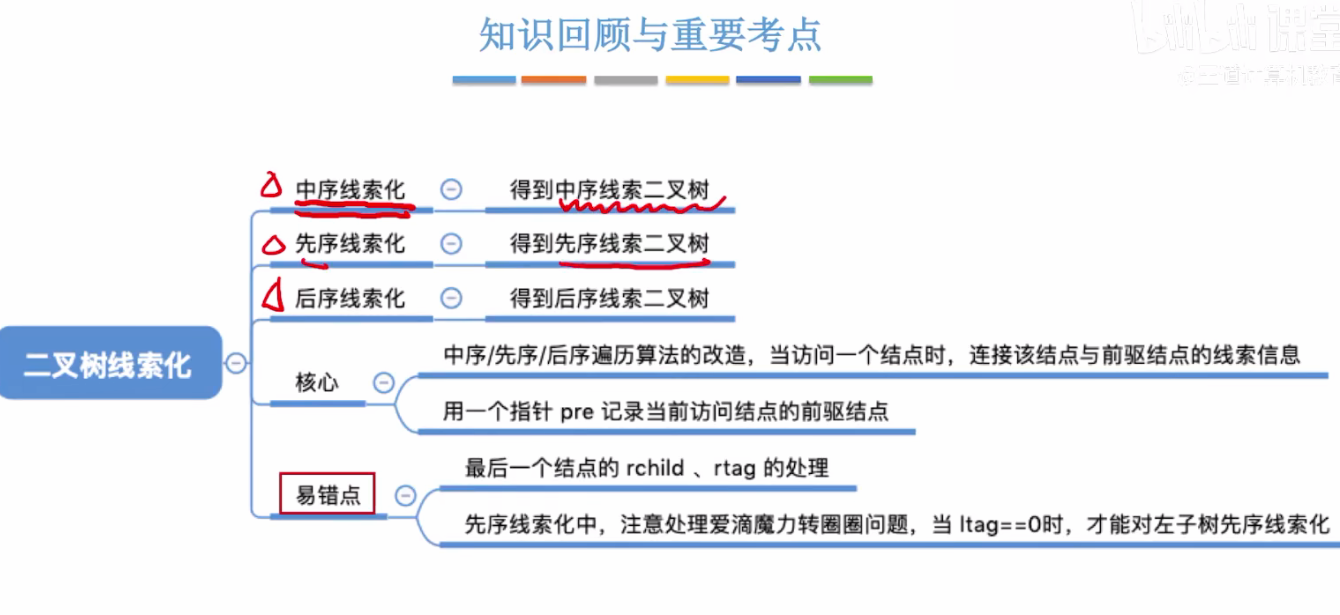
九、二叉树的线索化

1.用土方法找到中序前驱

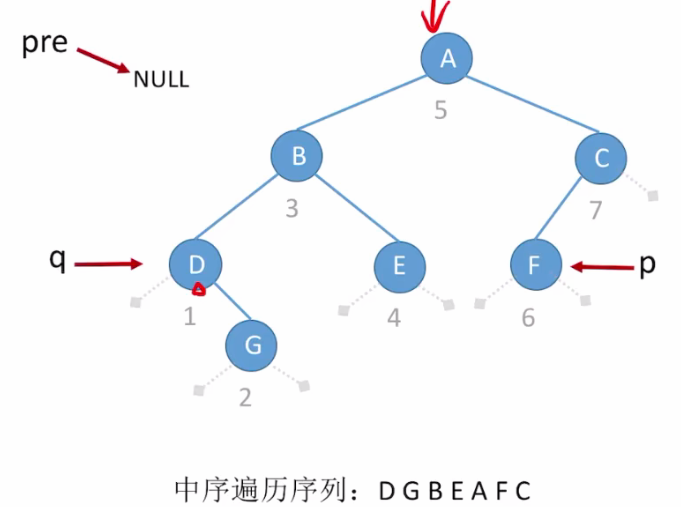
• 首先根据中序遍历找到第一个被 visit 的结点为D结点(定义为 q );
• 当前指针所指向的结点和最终要找的p结点不是一个,所以让 pre 指针也指向q指针指向的结点(即 pre 指向D)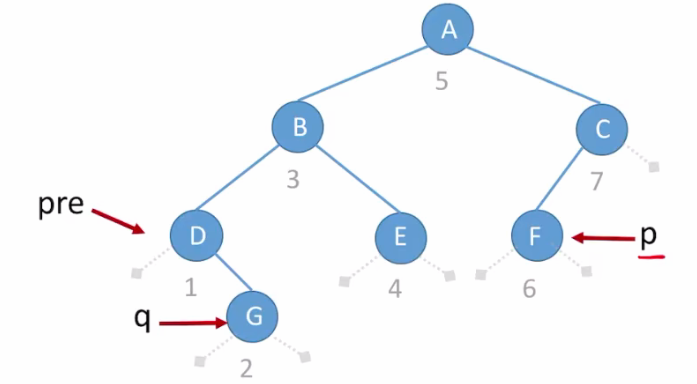
• 然后再进行遍历, q 指针下一个指向的为G结点;
• 此时 q 仍不等于 p ;则 pre 指针也指向G;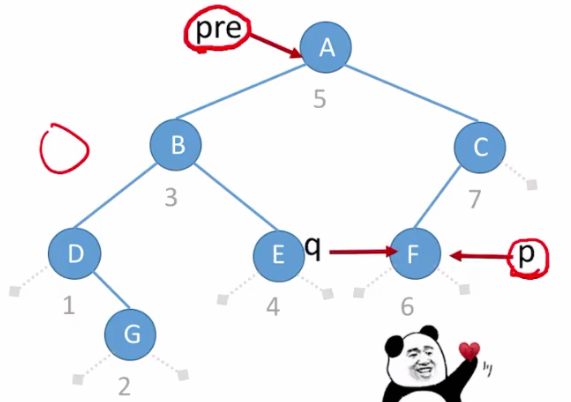
• 继续遍历,直到 q==p ;此时 pre 指向的A结点即为F的中序前驱

//中序遍历
void InOrder(BiTree T) {
    if (T != null) {
        InOrder(T->lchild);   //遍历左子树
        visit(T);             //访问根结点
        InOrder(T->rchild);   //遍历右子树
    }
}

//访问结点q
void visit(BiTNode* q) {
    if (q == p)       //当前访问结点刚好是结点p
        final = pre;  //找到p的前驱(pre)
    else
        pre = q;      //pre指向当前访问的结点

}

//辅助全局变量,用于查找结点p的前驱
BiTNode* p;              //p指向目标结点
BiTNode* pre = NULL;     //指向当前访问结点的前驱
BiTNode* final = NULL;   //用于记录数据最终结果

2.中序线索化

中序遍历顺序：D -> B -> E -> A -> F -> C -> G

⏳ 正在初始化演示数据...

特点

中序线索化后，树变成了一个"双向链表"结构。

(1)代码解释

//中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T) {
    if (T != NULL) {
        InThread(T->lchild);
        visit(T);
        InThread(T->rchild);
    }
}
void visit(ThreadNode* q) {
    if (q->lchild == NULL) {
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL) {
        pre->rchild = q;
        pre->rtag = 1;
    }
}

(2)图解代码

InThread函数相当于上面的中序遍历, 然后在visit函数中:

if (q->lchild == NULL) {
    q->lchild = pre;
    q->ltag = 1;
}
pre = q;

如上图:

• 如果q指针所指向的结点的左子树为空,则建立前驱线索,且令 ltag = 1;得到下图:

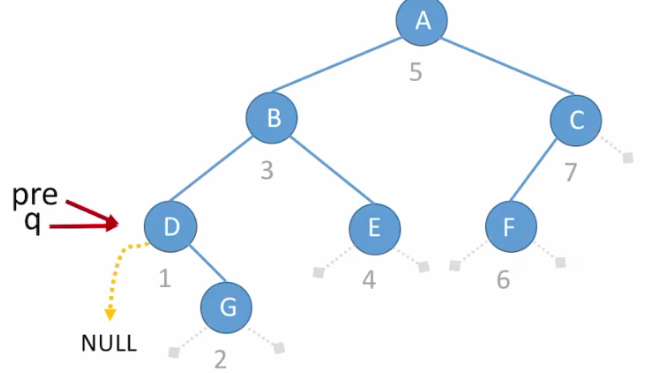
• 下一步,遍历到结点G,左孩子为空,所以左线索依旧指向 pre ,同时把对应的 tag 值设为1;得到下图:

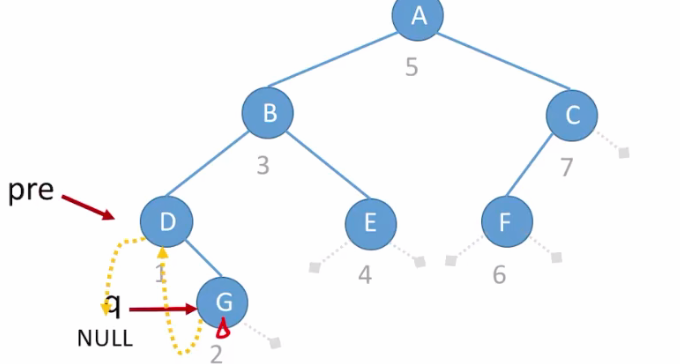
• 此时 pre!=null ,但是 pre 指针指向的结点有右孩子(G),所以D结点没有右线索;继续遍历:

如上图:

• 此时满足pre != NULL && pre->rchild,所以G结点的右线索指向q指针指向的位置(B结点),且令 rtag = 1;

• 继续遍历,得到最终结果:

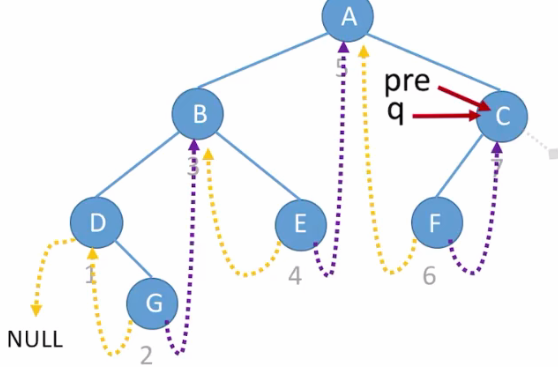
• 但是此时 C结点 没有右线索,所以最后要检查 pre 的rchild 是否为NULL,如果是,则令 rtag=1;

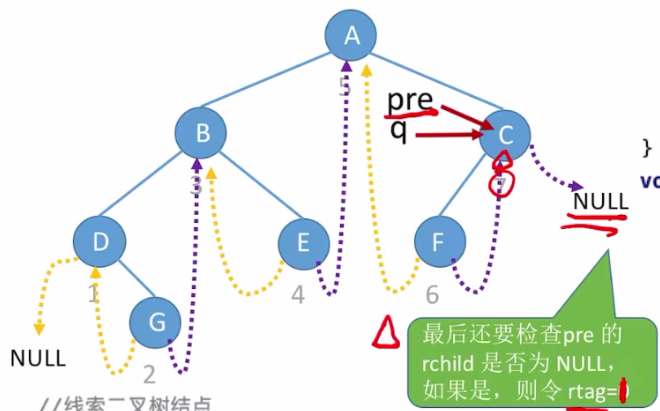
3.先序线索化

先序遍历顺序：A -> B -> D -> E -> C -> F -> G

⏳ 正在初始化演示数据...

注意

在先序线索化中，要特别注意左指针的处理，防止出现死循环（即左孩子是线索指向前驱，前驱又是自己，导致死循环）。

(1)代码解释

//全局变量 pre ,指向当前访问结点的前驱
ThreadNode* pre = NULL;

//先序遍历二叉树,一边遍历一边线索化
void PreThread(ThreadTree T) {
    if (T != NULL) {
        visit(T);
        if(T->latg==0)     //lchild不是前驱线索
            PreThread(T->lchild);
        PreThread(T->rchild);
    }
}

void visit(ThradNode* q) {
    if (q->lchild == NULL) {
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL) {
        pre->rchild = q;
        pre->rtag = 1;
    }
    pre = q;
}

void CreatePreThread(ThreadTree T) {
    pre = NULL;               //pre 初始为NULL
    if (T != NULL) {          //非空二叉树才能线索化
        PreThread(T);         //先序线索化二叉树
        if (pre->rchild == NULL)
            pre->rtag = 1;    //处理遍历的最后一个结点
    }
}

(2)图解代码

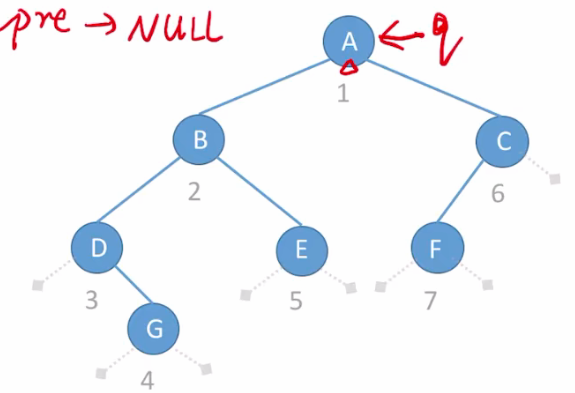如上图所示:

• 根据先序遍历的规则,从头开始遍历A结点;则q指针指向A结点,因为A结点的左右孩子都不为空,所以直接让 pre=q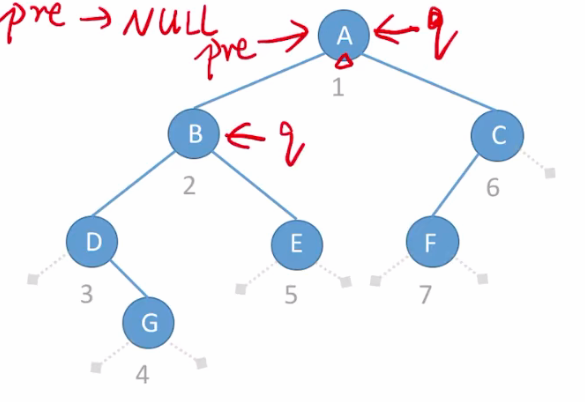 . 如上图:
• 继续遍历左孩子,让q指针指向B结点 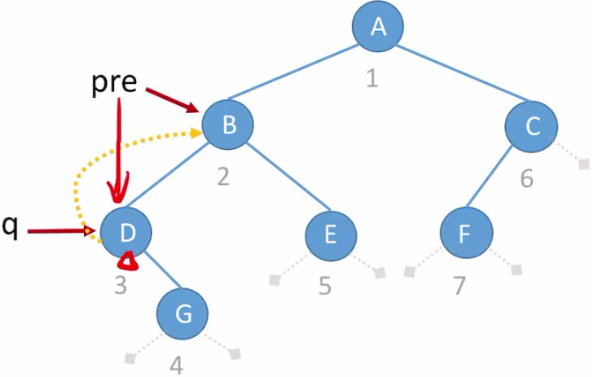如上图:此时遍历第三个结点
• q指针指向D结点,D结点没有左孩子,则左线索指向pre指针指向的结点,即B结点;
• 根据先序遍历规则,此时应该访问左子树,则q指针会再一次指回B结点
• 此时就会出现循环,原地打转

(3)注意点

如何规避这种情况?

• 我们只需观察 ltag ,如果 ltag==0 ,则说明lchild不是前驱线索

//先序遍历二叉树,一边遍历一边线索化
void PreThread(ThreadTree T) {
    if (T != NULL) {
        visit(T);
        PreThread(T->lchild);
        PreThread(T->rchild);
    }
}

变为:

//先序遍历二叉树,一边遍历一边线索化
void PreThread(ThreadTree T) {
    if (T != NULL) {
        visit(T);
        if(T->latg==0)    //lchild不是前驱线索
            PreThread(T->lchild);
        PreThread(T->rchild);
    }
}

4.后续线索化

后序遍历顺序：D -> E -> B -> F -> G -> C -> A

⏳ 正在初始化演示数据...

//全局变量pre.指向当前访问结点的前驱
ThreadNode *pre = NULL

//后序遍历二叉树,一边遍历一边线索化
void PostThread(ThreadTree T) {
    if (T != NULL) {
        PostThread(T->lchild);
        PostThread(T->rchild);
        visit(T);
    }
}

void visit(ThreadNode* q) {
    if (q->lchild == NULL) {   //左子树为空,建立前驱线索
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL) {
        pre->rchild = q;    //建立前驱结点的后继线索
        pre->rtag = 1;
    }
    pre = q;
}

//后序线索化二叉树T
void CreatePostThread(ThreadTree T) {
    pre = NULL;
    if (T != NULL) {           //非空二叉树才能线索化
        PostThread(T);         //后序线索化二叉树
        if (pre->rchild == NULL)
            pre->rtag = 1;     //处理遍历的最后一个结点
    }
}

5.总结