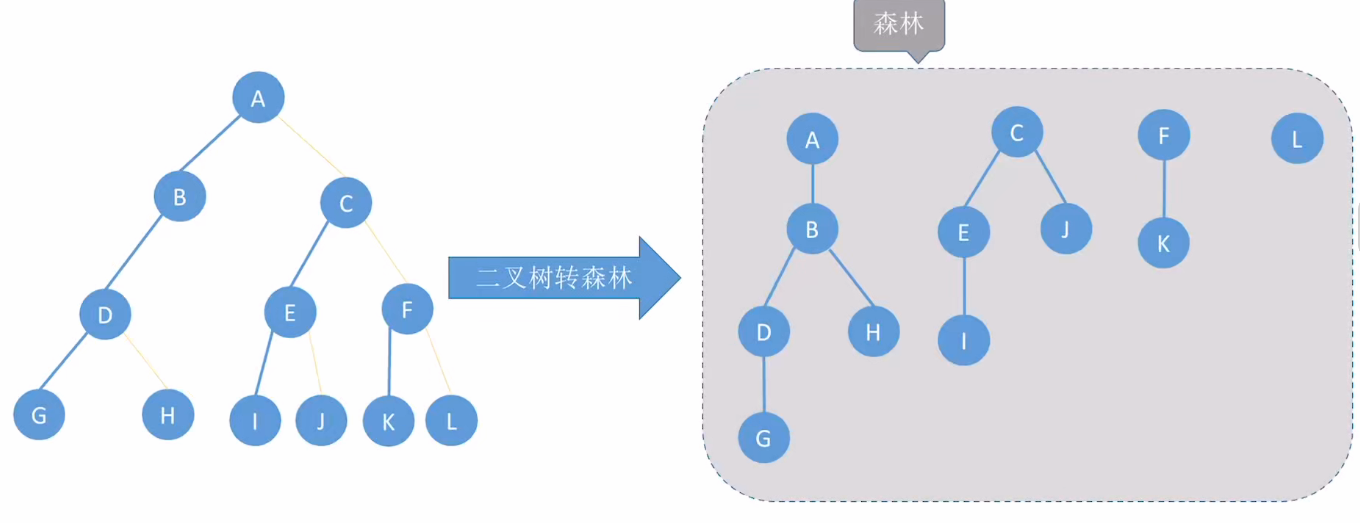
十二、树,森林与二叉树之间的转换
树与二叉树的转换演示
Step 1/4初始状态：普通树。每个节点可能有多个孩子。
1// 树 ➜ 二叉树 核心逻辑2// 暂略伪代码，请关注右侧图形变换1.树 -> 二叉树的转换
(1)技巧
- 树->二叉树的转换技巧 ① 先在二叉树中，画一个根节点。 ② 按“树的层序”依次处理每个结点。
- 处理一个结点的方法是：如果当前处理的结点
在树中有孩子，就把所有孩子结点“用右指针串成糖葫芦”，并在二叉树中把第一个孩子挂在当前结点的左指针下方。
(2)图解
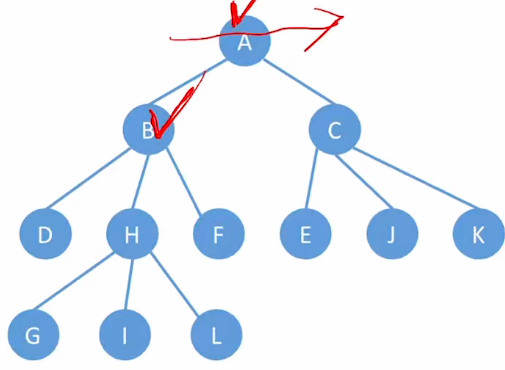如上图所示:
- 首先,写出来根结点A;
- 然后发现A结点有孩子,所以把所有孩子结点“用右指针串成糖葫芦”;
- 再把第一个孩子,也就是B结点挂在A结点的左指针下方.
得到下图:
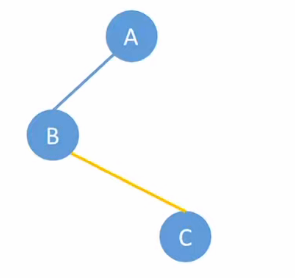{: height="150px"}
然后处理B结点: - B结点有3个孩子,将3个孩子用右指针串成一串,再将第1个孩子D用左指针挂在B结点下方;
得到下图:
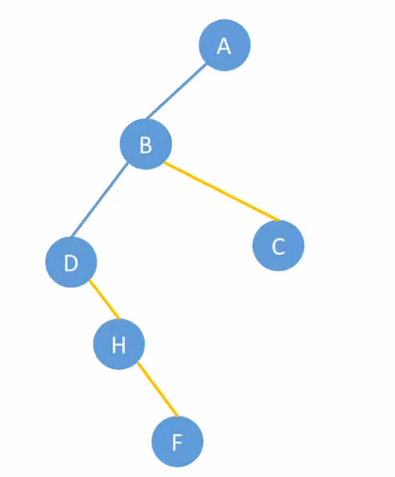{: height="200px"}
按照此方法,最终得到:
{: height="250px"}
2.森林 -> 二叉树的转换
(1)技巧
- 森林→二叉树转换技巧：
① 先把所有树的根结点画出来，在二叉树中用右指针
串成糖葫芦。 ② 按“森林的层序”依次处理每个结点。 - 处理一个结点的方法是：如果当前处理的结点在树中有孩子，就把所有孩子结点“用右指针串成糖葫芦”，并在二叉树中把第一个孩子挂在当前结点的左指针下方。
(2)图解
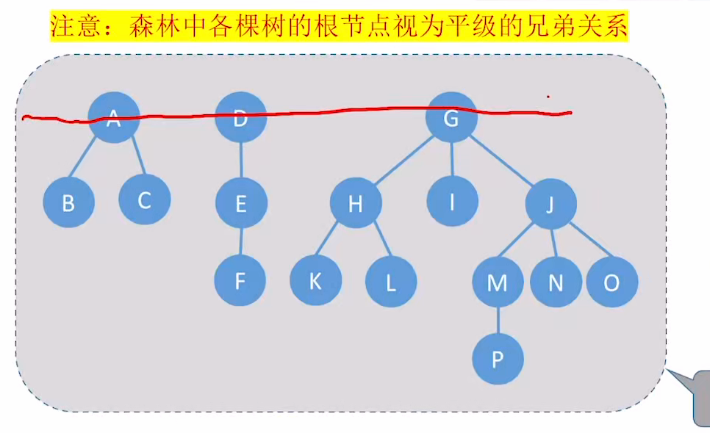
- 首先,将平级的根结点用右指针串起来
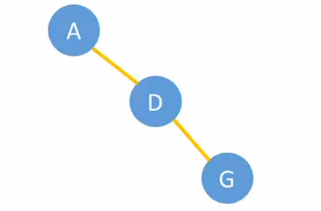{: height="100px"} - 然后处理B结点: B结点存在一个右兄弟--C结点,所以将其用右指针连在B结点下方;
- 再处理D结点: D结点只有一个孩子E,没有右兄弟,所以将E结点用左指针连在D结点下方;
- 这两步得到下图:
{: height="150px"}
按照此方法:
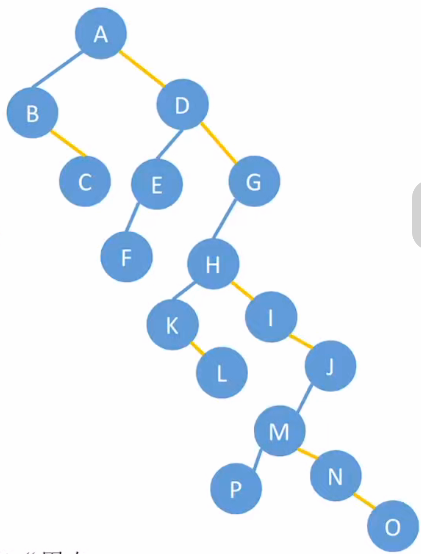
(3)示例
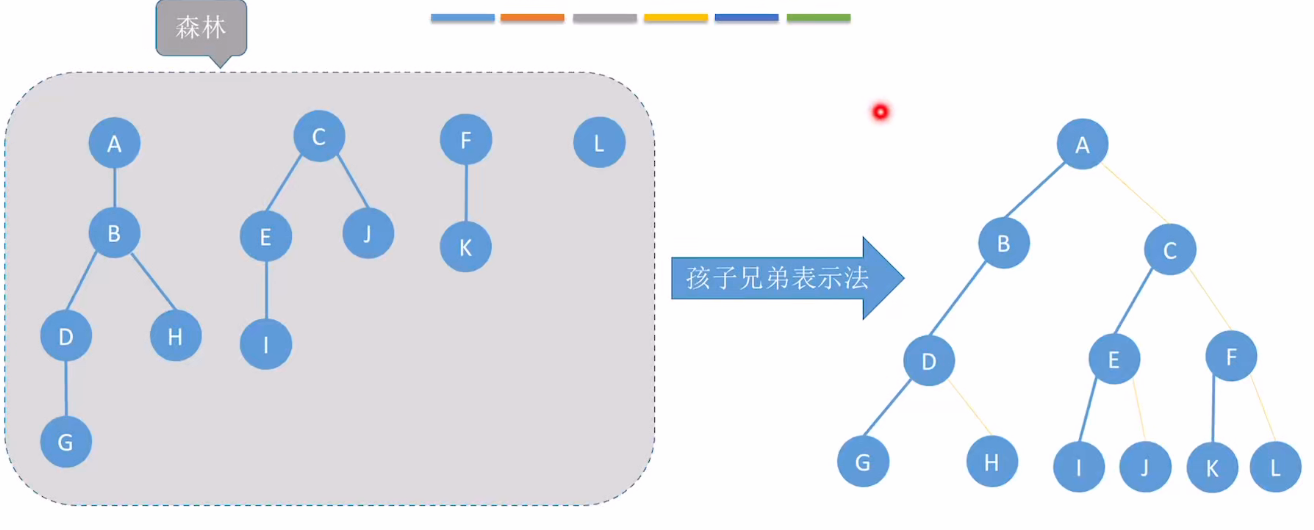
3.二叉树 -> 树的转换
(1)技巧
- 二叉树→树转换技巧： ① 先画出树的根节点 ② 从树的根节点开始，按“树的层序”恢复每个结点的孩子
- 如何恢复一个结点的孩子： 在二叉树中，如果当前处理的结点有左孩子，就把左孩子和“一整串右指针糖葫芦”拆下来，按顺序挂在当前结点的下方。
(2)图解
{: height="300px"}
如上图所示:
- 首先,右指针连的B,C结点拆下来;接到A结点下方,是A结点的左右孩子;
- 然后,右指针连的DHF结点拆下来,同样是B结点的3个孩子;
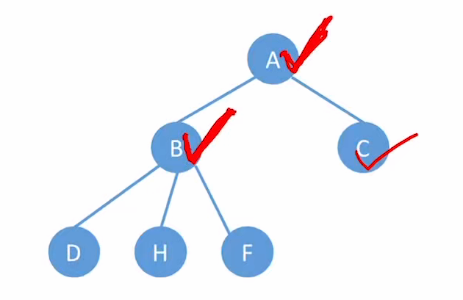
- 再观察,D结点的左指针为空,所以D结点是没有孩子的,不需要做恢复处理;
最终得到:
4.二叉树 -> 森林的转换
(1)技巧
- 二叉树→森林转换技巧： ① 先把二叉树的根节点和“一整串右指针糖葫芦”拆下来，作为多棵树的根节点 ② 按“森林的层序”恢复每个结点的孩子
- 如何恢复一个结点的孩子：在二叉树中，如果当前处理的结点有左孩子，就把左孩子和“一整串右指针糖葫芦”拆下来，按顺序挂在当前结点的下方。
(2)图解
{: height="300px"}
- 首先,将右指针连的3
个结点展开为根结点; 观察二叉树中,A的左指针指向B,B的右指针指向C;将BC一起拆下来,连到A的下面;观察:D的左指针指向E,而E没有右指针;说明E是D的唯一一个孩子;观察:G的左指针连到H,H的右指针连到IJ;说明HIJ为G的孩子;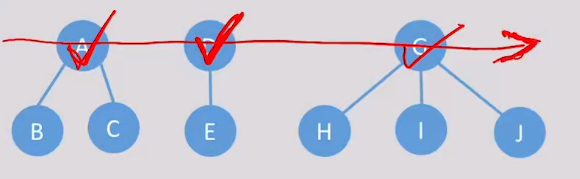
最终得到:
(3)示例
