八、字符串模式匹配
字符串模式匹配:自定义演练场
在这里,你可以自己输入字符串,实时观察 BF 算法和 KMP 算法的执行区别。
- 输入主串
S: "aaabaaaab" - 输入模式串
T: "aaaab" - 切换 BF 和 KMP,观察 KMP 是如何利用 Next 数组跳过不必要的比较的。
1int Index_BF(String S, String T) {2 int i=0, j=0;3 while(i < S.len && j < T.len) {4 // 1. 比较当前字符5 if(S[i] == T[j]) {6 i++; j++; // 匹配,后移7 } else {8 // 2. 失配,回溯9 i = i - j + 1; 10 j = 0;11 }12 }13 if(j >= T.len) return i - T.len; // 成功14 else return -1;15}1. 朴素模式匹配算法
(1)核心思想
- 将主串中所有长度为 m(模式串长度)的子串依次与模式串对比,直到找到匹配子串或遍历所有子串(最多匹配
n-m+1个子串,n 为主串长度)。

(2)字符串基本操作实现匹配
- Index(S,T):定位操作。若主串 S 中存在与串 T 值相同的子串,则返回它在主串 S 中第一次出现的位置;否则函数值为 0
int Index(SString S, SString T) {
int i = 1, n = StrLength(S), m = StrLength(T);
SString sub;
while (i <= n - m + 1) {
SubString(sub, S, i, m); //取出从位置i开始,长度为m的子串
if (StrCompare(sub, T) != 0) //子串与模式串对比,若不匹配,则匹配下一个子串
i++;
else
return i; //返回子串在主串中的位置
}
return 0; //S中不存在与T相等的子串
}
(3)数组下标实现匹配
- 图解代码
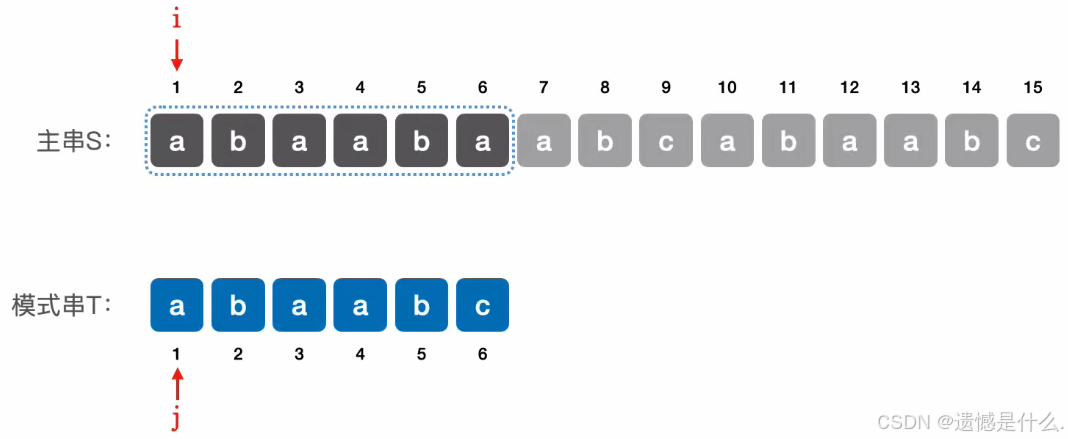
首先设计两个指针指向各个串的第一个位置,如果这两个字符相等,则指针后移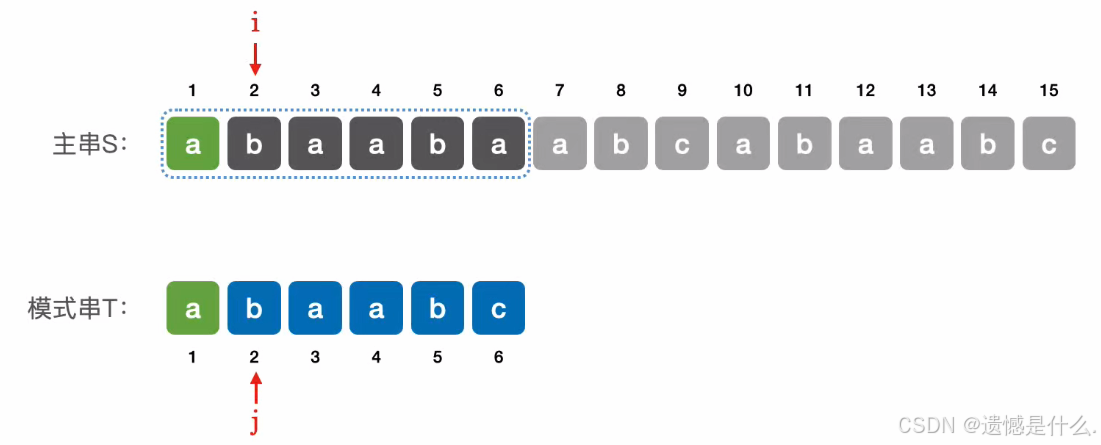
现在i和j指向的字符依旧相等,则继续后移,即i++,j++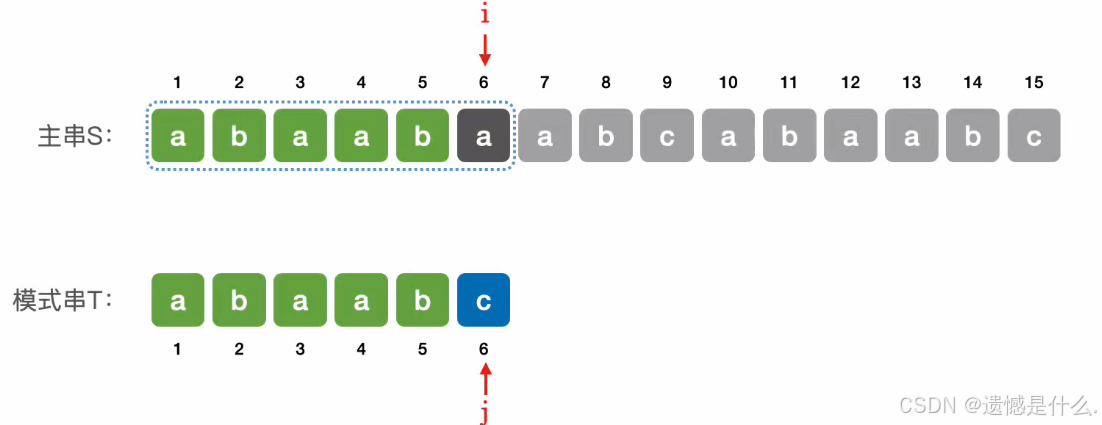
到第六个位置时,i和j指向的字符不相等,则没有匹配上;若当前子串匹配失败,则主串指针i指向下一个子串的第一个位置,模式串指针j回到模式串的第一个位置,即:
i = i - j + 2;
j = 1;
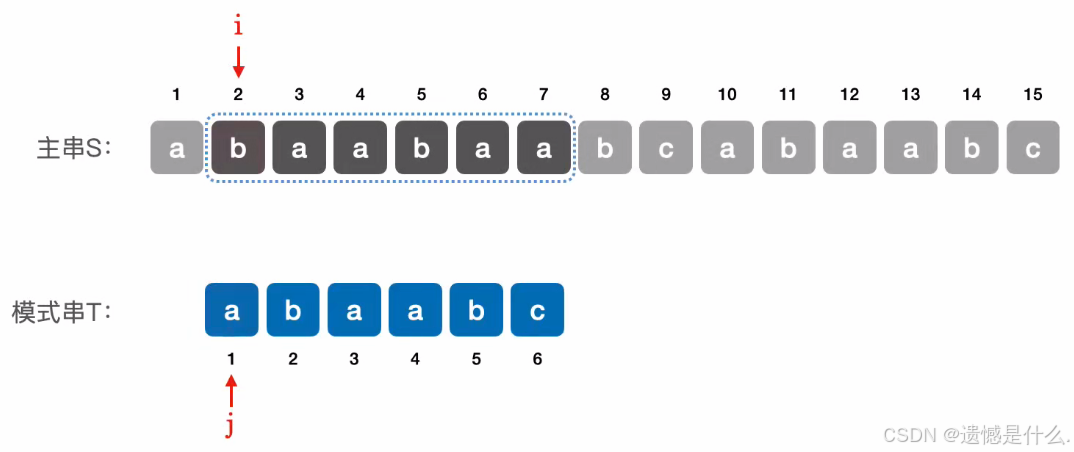
如上图所示:
主串S的指针 i 回到2的位置,模式串T的指针 j 依旧指向1的位置
现在两个指针指向的位置依旧不匹配,则 i 指针继续往后移动,j 指针依旧指向1;
i = i - j + 2; i = 2-1+2 = 3
j = 1; j = 1
————————————————
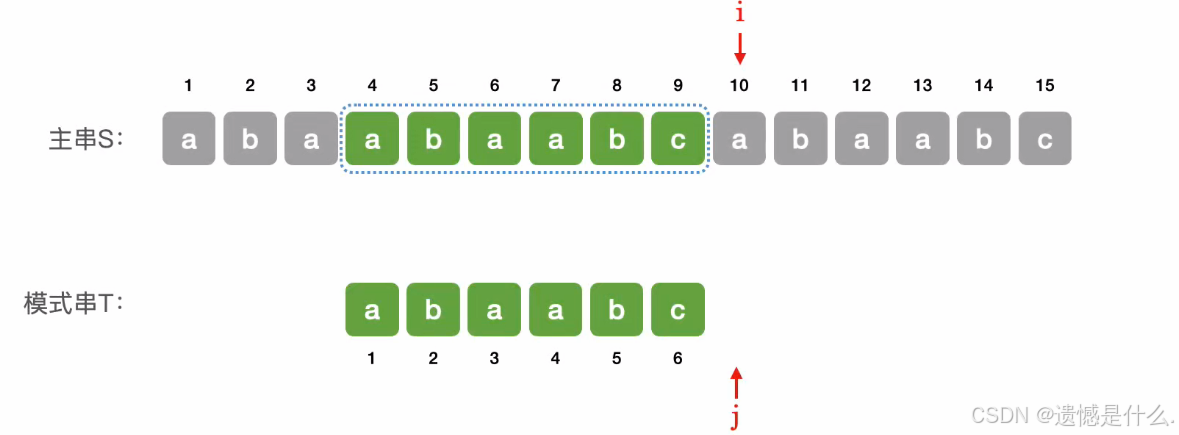
如上图所示:
- 每当发现 i 和 j 所指向的字符一样时,都让 i 和 j 往后移一位,如图,此时 j 指向的位置已经超越了模式串的长度,那这种情况下我们就说明当前子串匹配成功 ,即 j > T.length ,返回当前子串第一个字符的位置,即 i -T.length = 10-6=4
————————————————
- 完整代码
int i = 1, j = 1;
while (i < S.length && j < T.length) {
if (S.ch[i] == T.ch[j]) {
i++;
j++;
}
else {
i = i - j + 2;
j = 1;
}
}
if (j > T.length)
return i - T.length;
else
return 0;
}
- 最坏时间复杂度:
O(nm)(每个子串都需对比 m 个字符)。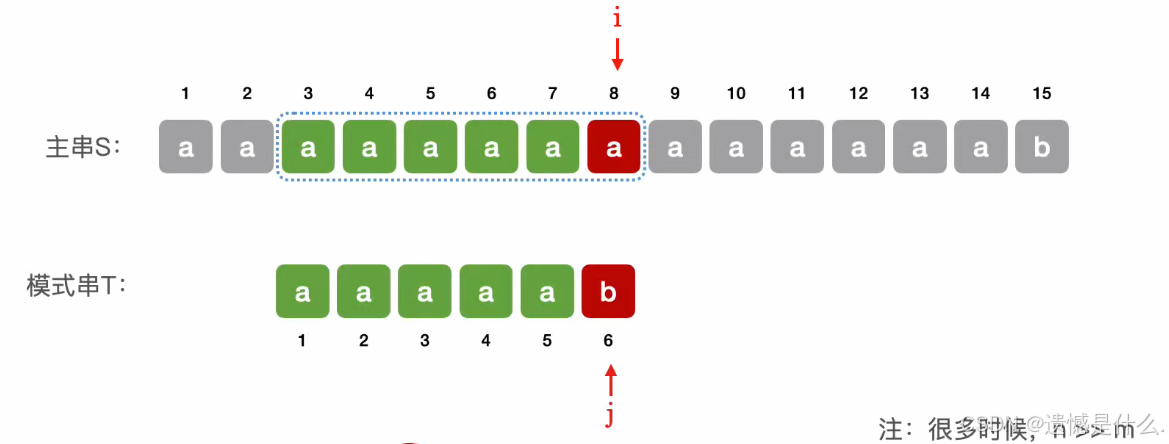
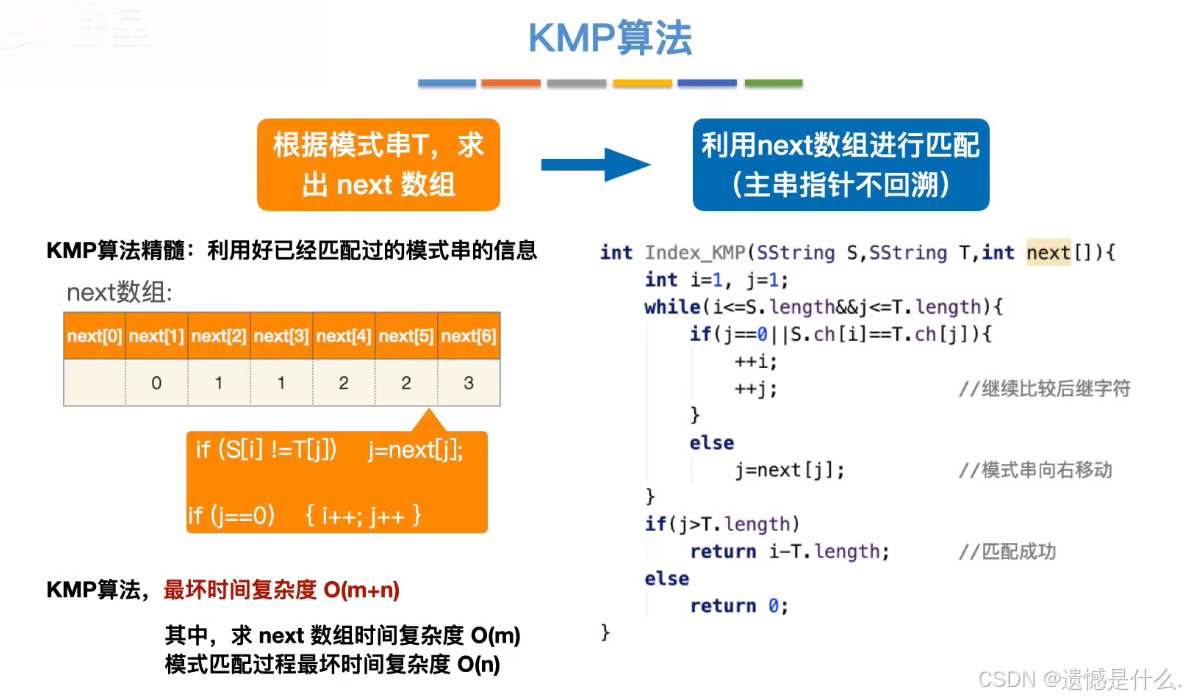
2. KMP算法
1.图解代码
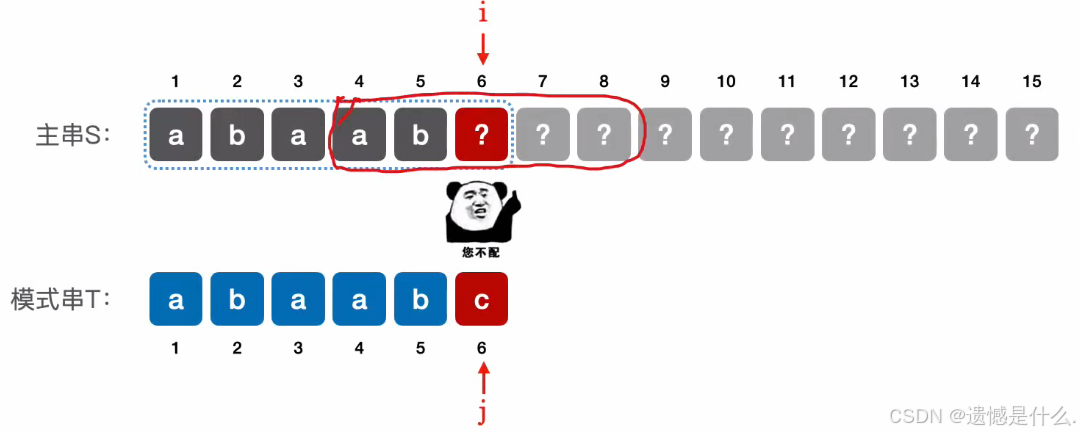
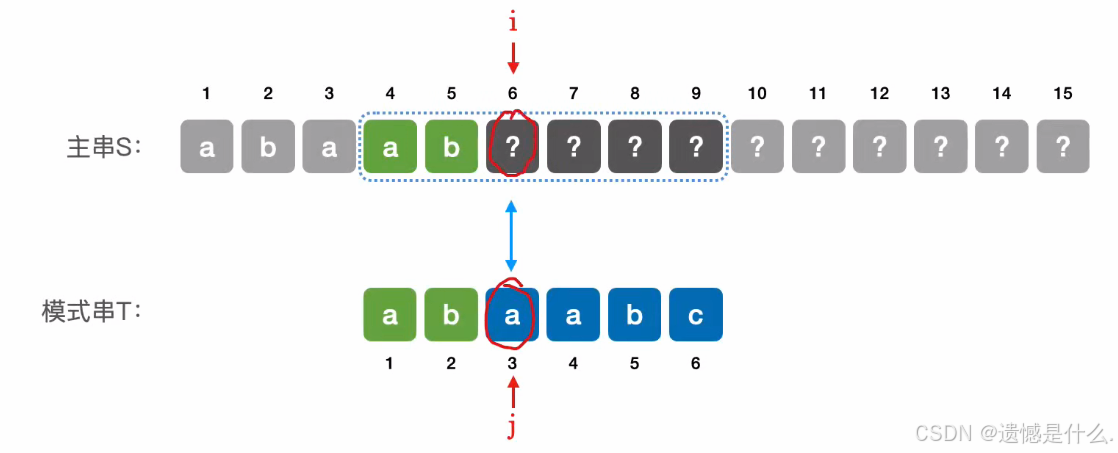
所有可以直接从如上图所示位置开始匹配, 可令主串指针 i 不变,模式串指针 j =3
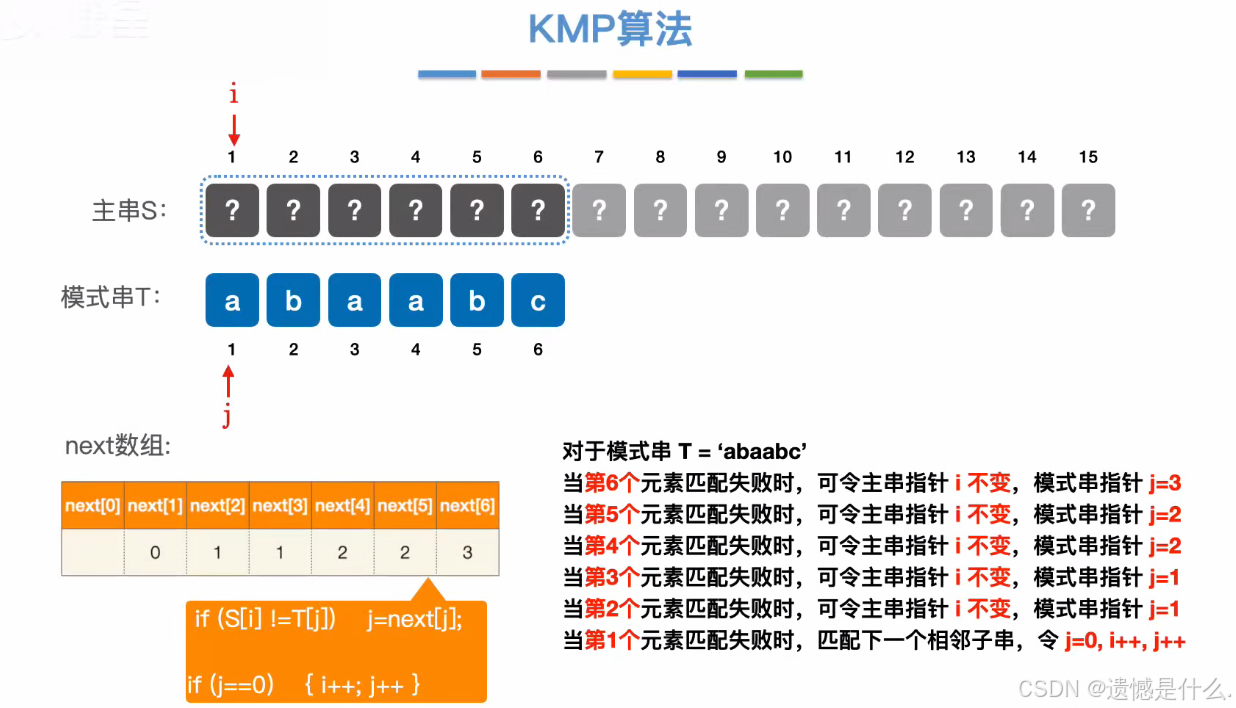
对于模式串 T = “abaabc”:
- 当第 6 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 3;
- 当第 5 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 2;
- 当第 4 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 2;
- 当第 3 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 1;
- 当第 2 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 1;
- 当第 1 个元素匹配失败时,匹配下一个相邻子串,令 j = 0,i++,j++。
2.示例代码图解
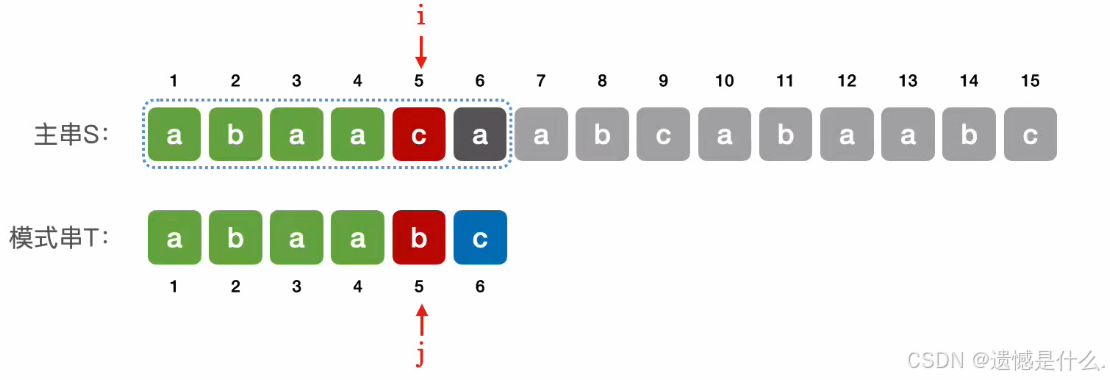
⇖ 当第 5 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 2; ⇙
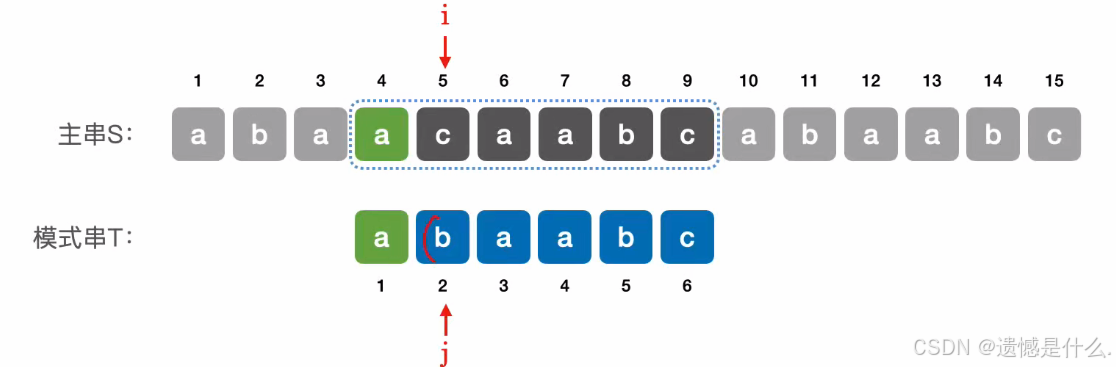
⇖ 当第 2 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 1; ⇙
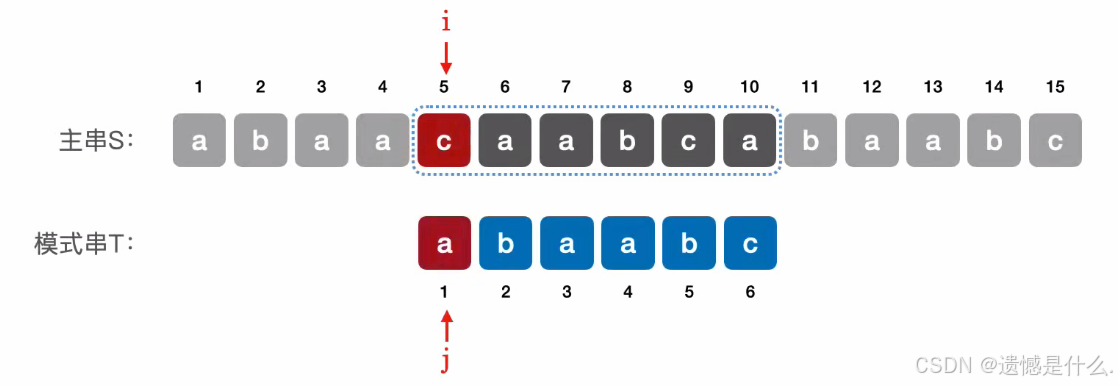
⇖ 当第 1 个元素匹配失败时,匹配下一个相邻子串,令 j = 0,i++,j++; ⇙
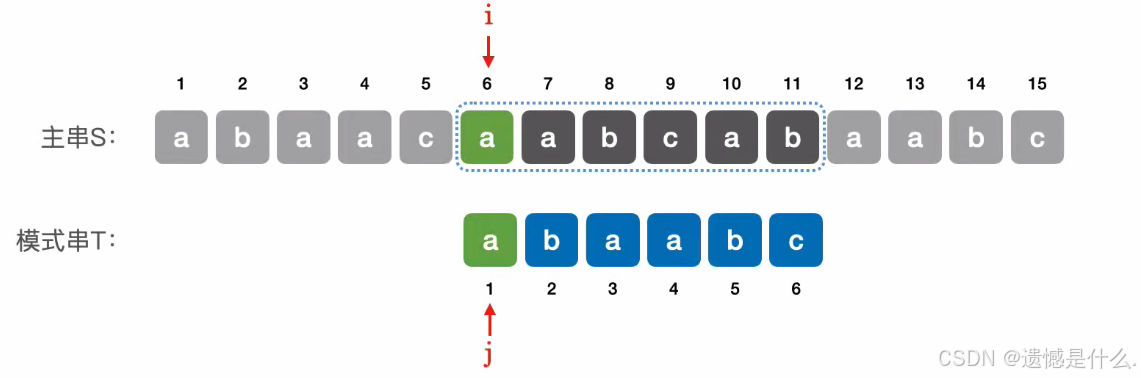
⇖当第 2 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 1 ; ⇙
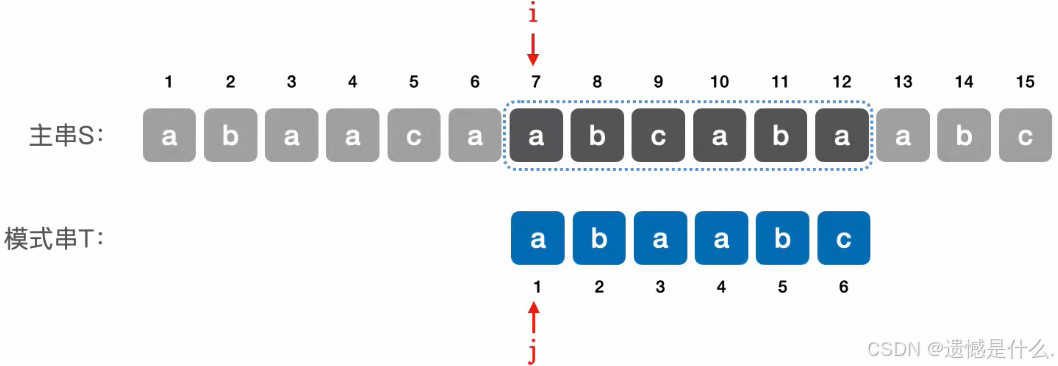
⇖ 当第 3 个元素匹配失败时,可令主串指针 i 不变,模式串指针 j = 1;⇙
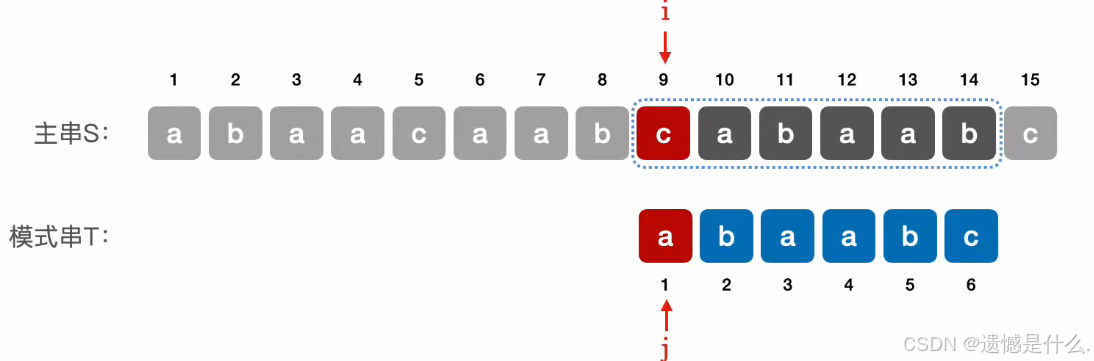
⇖ 当第 1 个元素匹配失败时,匹配下一个相邻子串,令 j = 0,i++,j++;⇙
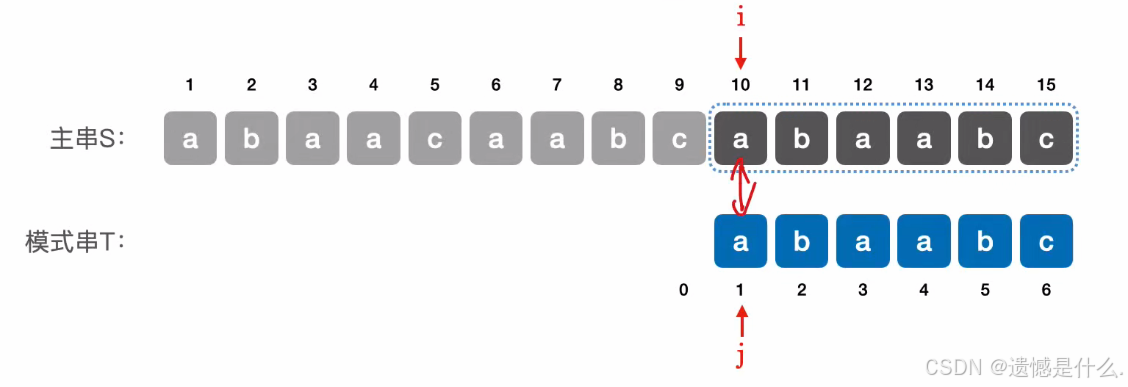
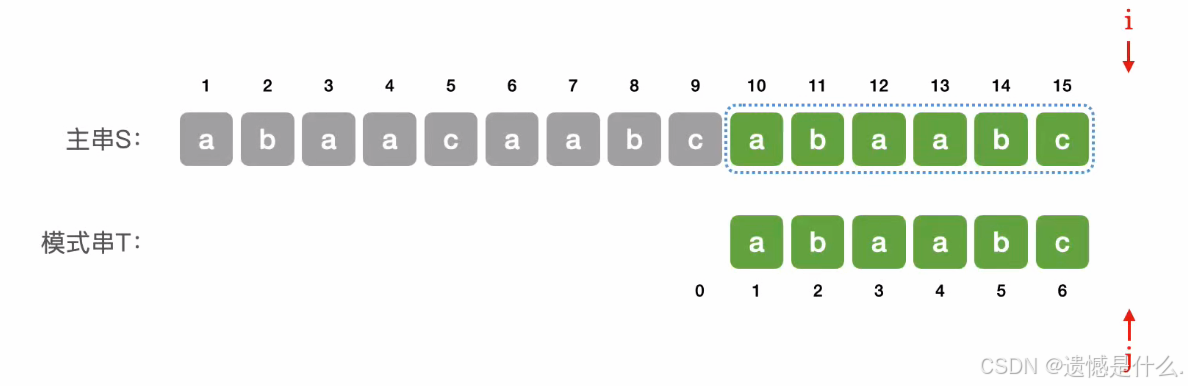
最终因为 j 超过了模式串的范围而停止匹配.
优化后,主串指针不"回溯",相比于朴素模式.
————————————————
3.完整代码
int Index_KMP(SString S, SString T, int next[]) {
int i = 1, j = 1;
while (i <= S.length && j <= T.length) {
if (j == 0 || S.ch[i] == T.ch[j]) { //如果主串和模式串的当前元素相等,则继续往后匹配
i++;
j++;
}
else {
j = next[j];
}
}
if (j > T.length)
return i - T.length;
else
return 0;
}
4.时间复杂度
- 求
next数组:O(m); - 模式匹配过程:
O(n); - 最坏时间复杂度:
O(n+m)。